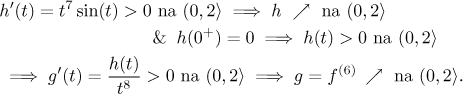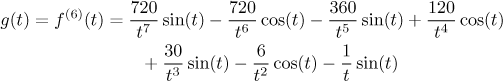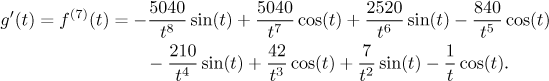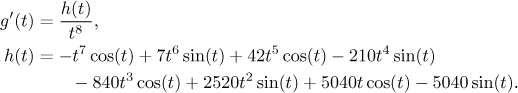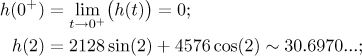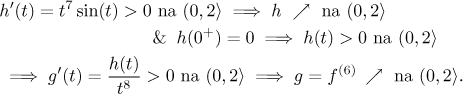Zde ukážeme, že funkce

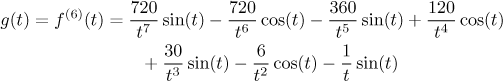
je rostoucí na intervalu M = (0,2⟩. Začneme pozorováním, že žádnou monotonii nevidíme přímo. Protože je cos(t) klesající a t^k rostoucí na M, je tam podíl cos(t)/t^k klesající. Takovéto členy jsou v našem g s plusy i mínusy a víme, že rozdíl dvou klesajících funkcí může být jakýkoliv, klesající, rostoucí nebo třeba vůbec nebýt monotonní; a navíc jsou tam ještě členy se sinem, což ukazuje, že tento přístup nikam nevede. Zdá se, že nějaký jiný algebraický přístup není, takže to zkusíme tradičním způsobem přes derivaci.

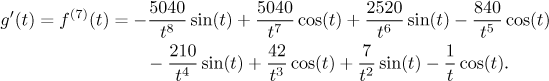
Je nemožné vyřešit g′ = 0 algebraicky, jedinou šancí je najít alespoň přibližná řešení numericky, ale i to by bylo dost trikové a obtížné. Musíme se tedy uchýlit k nestandardní taktice a trikům. Klíčovým je zde to, že vlastně tu rovnici nepotřebujeme řešit, potřebujeme jen ukázat, že g′ > 0 na M. Začneme tím, že si tuto derivaci přepíšeme na společný jmenovatel.

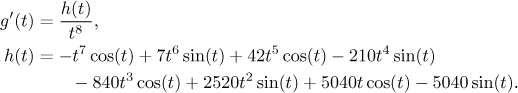
Protože je jmenovatel kladný stačí dokázat, že i čitatel h je kladný na M. A zase, dělat to nějak algebraicky se zdá nemožné, takže zkusíme vyšetřit, jak h jde; aplikujeme zde standardní přístup. Nejprve najdeme jeho derivaci a zde se stane malý zázrak. Každý člen se derivuje pomocí součinového pravidla a vzniknou dva členy. Úžasnou náhodou se sousední členy vykrátí a celý dlouhý výraz (celkem 15 členů) zkolabuje. Ověřte, že

h′(t) = t⁷sin(t).

Tohle je na M kladné, takže sama h je tam rostoucí. Proto je rozsah jejích hodnot určen hodnotami v koncových bodech.

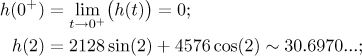
Vidíme, že na M jsou hodnoty h mezi 0 a 31, což mimo jiné značí, že h musí být kladné a důkaz je hotov.

Abychom ukázali, jak jednotlivé kusy této skládačky do sebe zapadají, tak tady stručně rekonstruujeme celý řetěz úvah.