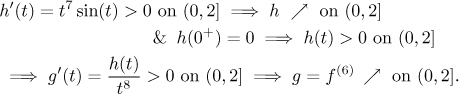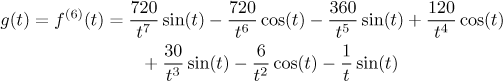
Here we will show that the function
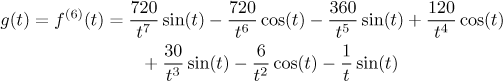
is increasing on the interval
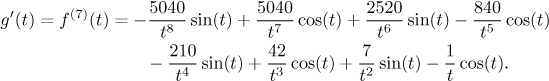
Solving
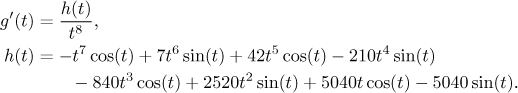
Since the denominator is positive, it is enough to prove that the numerator h is also positive on M. Again, doing it somehow algebraically seems impossible, so we do it by investigating how h goes; that is, we apply the standard monotonicity approach. First we find its derivative and here a little miracle happens. Each term is differentiated using the product rule and thus produces two terms. By a remarkable coincidence, neighboring terms cancel out and the whole long expression (15 terms in all) collapses on itself. Check that
This is clearly positive on M, so h itself is increasing there. Thus the range of values it can reach is given by values at the endpoints.
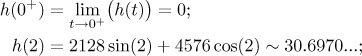
We see that on M the values of h are between 0 and 31, so in particular h must be positive and the proof is finished.
Just to show how all pieces of this puzzle fit together, we briefly reconstruct the chain of argument here.