Zde se podíváme na problém stěhování gauče. Předpokládám, že jste na link na tuto poznámku klikli dobrovolně a jste tedy dobrodružné povahy, tudíž vás trochu dobrodružnější matematika nezastraší. Zkusíme se proto na tuto otázku podívat zcela obecně.

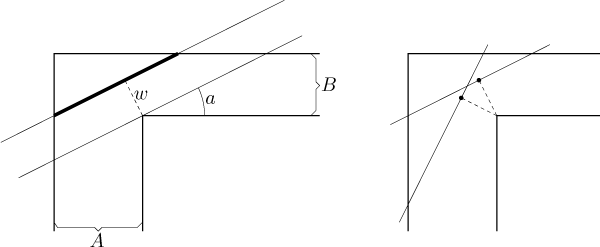
Chodba o šířce A metrů zahýbá do pravého úhlu do chodby o šířce B metrů. Chceme najít maximální délku, aby se objekt této délky a o šířce w metrů (w < A) dal protáhnout touto zatáčkou bez zvednutí z podlahy (leží naplocho).

Zkusíme se držet základní myšlenky toho jednoduššího problémku s w = 0. Představíme si dvě úsečky, které jsou rovnoběžné a w metrů od sebe, přičemž ta vnitřní se dotýká vnitřního rohu a mu se ptáme, kde se vnější úsečka dotýká vnějších zdí. Zdálo by se, že se vlastně posune pozice rohu o w a vnější úsečka se dotýká tohoto přesunutého rohu. To by nám umožnilo ignorovat tu vnitřní úsečku a pracovat jen s vnější, čímž by se výpočty zjednodušily. Dá se opravdu tento obecnější problém vyřešit prostě tak, že si představíme, že je roh někde jinde, a pak se odvoláme na výsledek toho jednoduššího problému?

Bohužel, není tomu tak, protože nová pozice rohu záleží na úhlu úsečky.

Ten nápad s ignorováním vnitřní úsečky a držením vnější ve správné pozici pomocí spojovací kolmé příčky o délce w je nicméně dobrý, protože to je v zásadě jediný rozumnější způsob, jak nějak popsat její pozici. Můžeme to tedy použít k nalezení nějakých struktur, které už dokážeme zpracovat, jmenovitě zkusíme trojúhelníky.

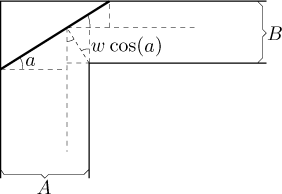
Z podobnosti mají tyto čtyři trojúhelníky na obrázku shodný úhel a, můžeme tedy vypočítat délku úsečky následujícím vzorcem:

Potřebujeme najít minimum této funkce na intervalu (0,π/2). Nemůžeme jej nějak najít jen analýzou vzorce udávajícího l, protože se v něm míchají siny (který tam roste) a kosiny (který je tam klesající). Zkusíme tedy standardní přístup přes kritické body.

Tato derivace je rovna nule pro a splňující

Asin³(a) − Bcos³(a) = w(sin²(a) − cos²(a)).

To je rovnice, kterou neumíme analyticky vyřešit, takže jsme skončili. A to nejen obecně, ale dokonce i kdybychom měli konkrétní hodnoty pro A, B a w, stejně bychom tuto rovnici ve většině případů neuměli vyřešit. Pokud bychom toto a opravdu potřebovali znát, museli bychom jej najít numericky pomocí vhodného software (nebo se jej rovnou zeptat na minimum l).

Jsou nějaké jednodušší případy, které bychom vyřešit uměli? Je jasné, že bychom to uměli vyřešit pro w = 0, protože pak máme případ, který řešíme ve Cvičení. Další jednoduchý případ je, když A = B. Rovnice se zjednoduší na

1 + sin(a)cos(a) = (w/A)(sin(a) + cos(a)),

to zde ale nepomůže, protože ani tuto nelze řešit přímo. Nicméně když se podíváme na tu původní rovnici, umíme uhodnout, že při A = B dostaneme rovnost, pokud sin(a) = cos(a). Je ale pravda, že ten úhel π/4 je něco, co bychom dokázali dostat i bez celé té komplikované práce, je to jen otázka selského rozumu. Jestliže A = B, pak je situace symetrická a proto také ke kritické chvíli dojde, když je úsečka v symetrické pozici, což dává následující situaci.

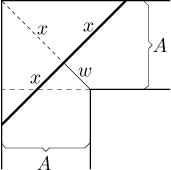
Můžeme tedy použít Pythagorovo pravidlo a dostaneme