Problem: Investigate boundedness and monotonicity of
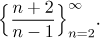
Solution:
We try to calculate the first few terms:
a2 = 4,
a3 = 5/2,
a4 = 2,
a5 = 7/4. The first impression is that the
sequence could be decreasing. What is the long term tendency? When n
is large, the parts "+2" and "−1" can be ignored (see
Intuitive calculations in
Theory - Limit) and we get n/n = 1. So the sequence
seems to go to 1, therefore it should be bounded (see the appropriate
theorem in
Theory - Limits - Basic
properties). Also, since 1 is less than
a5 = 7/4, it seems possible that this sequence
keeps going down. Thus we guess that it is decreasing.
Proof of boundedness:
First, clearly an > 0 for
n ≥ 2.
This shows that the sequence is bounded from below.
From our calculations above we guess that
an ≤ 4.
We will try to prove it.
Note that since we assume
n ≥ 2,
we are multiplying the inequality below by a positive
number; therefore we do not have to change the direction of this inequality
(we will make a note about it on the right).
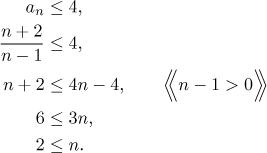
The last inequality is true for all
n ≥ 2.
Since the operations were equivalent, also the first
inequality is true, exactly as needed.
Proof of monotonicity:
Now we will try to prove that the given sequence is decreasing. Again, note
that we multiply out the inequality by positive numbers.

Since the last inequality is true and the operations were equivalent, the
first inequality must also be true and the monotonicity is confirmed.
We can also try to use methods from theory of functions. We pass to
investigation of functions (see
Sequences and functions in
Theory - Limits) and check on monotonicity of the function
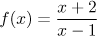 . We find the
derivative:
. We find the
derivative:
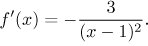
Since this derivative is always negative, the function f is decreasing
on (1,∞) and consequently
also our sequence is decreasing.
Next problem
Back to Solved Problems - Basic
properties
![]()
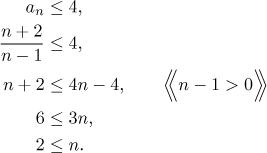

![]() . We find the
derivative:
. We find the
derivative:
![]()