Problem: Determine the domain of the following function:
![]()
Solution: There are no general powers to be rewritten, so we look at the function as it is given for problems. Going from the left:
1. The arcsine requires that the argument is from the interval
![]()
2. In the arcsin there is a fraction, the denominator cannot be zero,
so we get
3. Next we have the square root, its argument must be positive or zero:
![]()
4. The logarithm requires that its argument be positive:
![]()
5. The fraction in the logarithm needs a non-zero denominator:
6. The third term needs a non-zero denominator:
7. Finally we are getting to the logarithm on the right, its argument must be positive:
![]()
Then we have a root in the logarithm, but its argument
Now we have to determine the sets that correspond to these conditions. For conditions 2 and 5 no work is needed, so we look at the others.
Condition 1: This kind of double inequality can be solved two ways. One is to solve each inequality separately, which is best done by changing them to the type "some product/ratio of linear factors compared to 0". The resulting sets are then intersected, since we need both inequalities to be true simultaneously. We leave this method to the reader, since we use this method also in condition 3 where we show it. If you really need to see this, click here.
Here we prefer to show an alternative method, since we will not be using it anywhere else in this problem. We will multiply the double inequality by the denominator to get rid of fractions. However, for that we need to know the sign of the denominator, since negative case requires changing directions of the inequalities. Since the sign can be arbitrary, we need to split the real line to two regions, one where the sign is positive and one where the sign is negative, and solve the problem in each part separately. However, the solution in each part is valid only there, in the part where it was done, so anything that is outside must be disregarded.
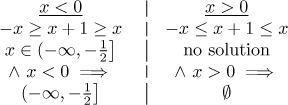
Since we have a free choice whether to try positive or negative denominator, we get the final answer by making a union of the partial answers. Thus the second condition means
![]()
Condition 3: By raising both sides of the equation to e and
cancelling
![]()
We can also see this by knowing the graph of logarithm.
This kind of inequality is best solved by getting zero on one side and factoring whatever comes up on the other side into linear factors.
![]()
The breaking points for signs of the factors are
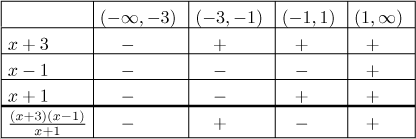
So the second and fourth intervals work for our inequality. Next we need to
check on the breaking points by substituting them into the expression on the
left and asking whether the inequality is satisfied. The points
![]()
Condition 4: We see that this condition is actually less restrictive than the condition we investigated in Condition 3, and since we will be intersecting these outcomes, these two conditions will yield the answer of Condition 3 anyway, there is no point working this one out.
Condition 6: Could it happen that sine hyperbolic is zero? Yes, if its
argument is zero. Thus this condition actually reads
Condition 7: This is in fact a bit tricky. We are facing an inequality
with a square root, so our first instinct might be to move
Thus probably the easiest method is through zero points. We start by solving equality instead of inequality:

Since squaring an equality is not an equivalent operation, we can get "false
solutions", so we first check on these two numbers. After substituting into
the original (non-squared) equality we see that
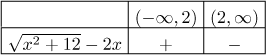
We see that the first interval is the region where the inequality is satisfied, it remains to see whether the interval should be closed or open. This is done simply by substituting the breaking point 2 into the inequality and we see that it does not work. Therefore the condition 7 reads
Now we need to make an intersection of all these conditions:
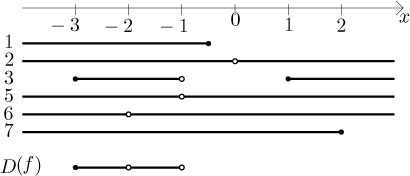
The solution is