Problem: Investigate boundedness of the following function:

Solution: This function is a sum of three terms, so we start by investigating each in turn. But first we determine the domain of this function. The first term requires that x∈[−1,1]. In the second term we have arcsine, which has the same requirement, and in the denominator we have x ≠ 1. In the third term we have a logarithm which requires x > 0, we also need to look at the denominator, but since the exponential is always positive, we have e^x + 1 > 1 and no trouble is possible. Therefore

D( f ) = (0,1).

The first term is a function with domain [−1,1] on which it is continuous, therefore by the Extreme value theorem it is bounded there. Consequently it is also bounded on the subset (0,1).

The second term is a ratio. The numerator is a product of arcsin, which is a bounded function, and the exponential, which is not a bounded function as a whole, but it is continuous and hence also bounded on the bounded closed interval [0,1], therefore also bounded on its subset (0,1). The product of two bounded functions is bounded, so the numerator is bounded on (0,1).

Now we need to check on the denominator. If it is separated from zero, we have a bounded fraction. Unfortunately, on the interval (0,1) the term x − 1 can get as close to 0 as required, which shows that we might be in trouble. Since the fraction is a continuous function on (0,1), we know that no problem can arise in the middle of this interval. Thus the whole issue will be decided by the behaviour of this fraction at the endpoints. We have no trouble at 0:

but we have some at the other end:

Thus this second term is not bounded on (0,1).

The third term needs to be investigated, even though we lost boundedness in the second term, since if this one also came out unbounded, it could onceivably happen that those two "unboundednesses" would cancel each other out.

The third term is a ratio again. Is the numerator bounded? The function x is continuous on [0,1], hence bounded there and also on (0,1). However, we know that logarithm runs away to negative infinity at 0⁺, so we might be in trouble. We could now check on the limit at 0 from the right of the whole fraction, but that would be unnecessary work, here boundedness of the fraction is determined solely by the behaviour of the numerator.

Indeed, if the numerator is bounded, then so is the whole fraction, since we already observed that the denominator is separated from zero, precisely, e^x + 1 > 1. On the other hand, if the numerator runs away to infinity at some endpoint, then so does the whole fraction, since the denominator is a nice continuous bounded function on [0,1], in other words, it does not provide any infinity at 0 or 1 that could cancel the infinity (if any) in the numerator.

So here we go. Just to be on the safe side we look at the right end, too, although we already saw that no problem arises there.

What is really interesting is the left end, but this is a textbook example:

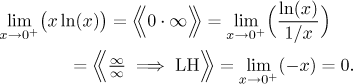
Since we've got finite limits at the endpoints, the numerator is bounded and therefore (due to the denominator separated from zero) also the whole fraction is bounded.

Now we come to the conclusion. The first and the third term is bounded, so these two cannot cancel the unboundedness we found in the second term. Therefore the given function is not bounded.

Next problem
Back to Solved Problems - Real functions