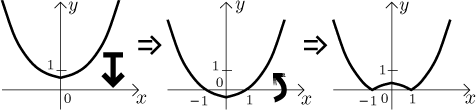
Problem: Using the knowledge of transformations guess the graph of the following functions:

Solution: As you can guess, this problem is "educational", we will try to make some point here. Since the only difference between the first two problems is the placement of the absolute value, it seems that we will focus on the order of transforms and the effect of mirroring here. Let's start with the first example.

a)     Clearly the basic function here is the exponential. We are applying two transformations to the argument, in the order of evaluation we first subtract 1 and then take the absolute value. Since transformations to argument should be applied "last to first", we should start with the graph of e^x, then mirror the positive half symmetrically to the left to account for the absolute value and then shift the resulting picture to the right by 1. We check that this order "mirroring-shift" is correct by the replacement trick.

x → |x| → |x − 1|.

This fits, so we do it.

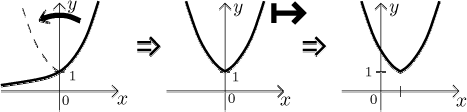
One quick check that we did not make any major screw-up: The function as given has a suspicious breaking point when the absolute value is zero, that is, when x = 1, which agrees with the picture, and the limit of f at infinity and negative infinity is infinity, which checks again.

b)     Now the second function. There the order is the opposite, when we evaluate the function, we first do the absolute value and then subtract, so the transformations should go "shift-mirroring". Quick check using the replacement:

x → x − 1 → |x| − 1.

This fits, let's go.

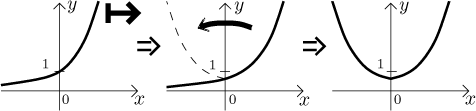
Quick check: The break in the absolute value happens when x = 0, this agrees with our picture.

c)     The third function is also based on the exponential. In fact we can start from the graph we just drew, then apply two more transforms to it. The function e^|x| − 1 is shifted down by 1 and then we take absolute value of it, and since transformations to the value are done in the same order as evaluation, this tells us what to do with the above graph. First we shift it down by 1, then we take whatever parts are below the x-axis and flip them around to the top.

Obviously, here it helps if we have some better idea concerning just what parts of the shifted exponential will be below the x-axis. In other words, we want to know which parts of the above graph are below the level y = 1. The original exponential reached level 1 at x = 0. After the shift, the level 1 was reached at x = 1, the mirroring effect added another such point, x = −1. Therefore, after shifting this resulting graph down by 1, it will be precisely the part on the interval (−1,1) that will go below the x-axis. Then it gets flipped up.

Back to Solved Problems - Real functions