First we will explore the solution by factoring and determinign signs. This is done by solving each inequality separately, changing them to inequalities with 0 on one side.
The left inequality can be changed to
![]()
We can divide the inequality by 3, so we see that we just need to determine the sign of the expression on the right and check where it is positive (or zero). Dividing points for factors are 3 and 9, so we get the following chart:

Now we see the intervals where the fraction is positive, substituting the dividing points into the fraction we also see that 9 makes no sense, so it is out, but 3 gives 0, which satisfies the given inequality and thus 3 should be included. Conclusion is that the left inequality has the solution
Now we need to look at the right inequality:
![]()
We work it out similarly as above:

The solution is
Now we need to put these two parts together. Since both inequalities must be true simultaneously, we take the intersection of the partial solutions, therefore the solution to the double inequality is
Alternative solution:
Now we try to start by getting rid of the fraction, which is done by
multiplying the whole inequality chain by

In each part of the real line we now solve two inequalitites, but these are very simple. Since we want the two inequalities to work simultaneously, we intersect the two solutions, but then we also have to intersect the result with the region in which the work was done.
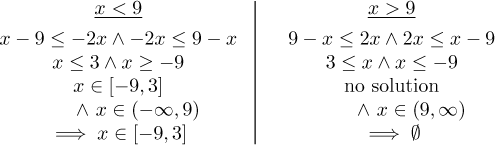
Since we have a choice what x to try, whether