Tečny a normály
Je mnoho způsobů, jak určit rovnici přímky v rovině. V naší situaci budeme
hledat rovnici přímky, která prochází jistým bodem
(a,b) a má směrnici k. Rovnice pak je
y − b = k⋅(x − a).
Protože bod leží na grafu dané funkce f, máme
b = f (a).
Směrnice tečny ke grafu je dána
kT = f ′(a),
aby tato přímka i křivka měly v daném bodě stejný směr. Dostaneme tak
rovnici tečny:
y − f (a) = f ′(a)⋅(x − a).
Jak dostaneme normálu? Její směr je kolmý na tečnu, proto její směrnici
dostaneme z následujícího faktu.
Fakt.
Uvažujme dvě přímky v rovině, jejichž směrnice jsou k1
a k2. Tyto dvě přímky jsou navzájem kolmé tehdy a jen
tehdy, když
k1⋅k2 = −1.
Dostaneme tedy následující vzorec pro směrnici normály:
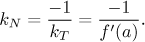
Proto je rovnice normály tato:
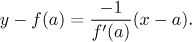
Pro příklad viz
Tečna v Přehledu metod -
Aplikace, podívejte se také na Řešené příklady -
Aplikace.
Poznamenejme, že vzorec
kN = −1/kT
zahrnuje také případy, kdy je jedna z těchto směrnic nekonečná (svislá
přímka) a druhá je nula (vodorovná přímka).
Rovnice přímky se dá napsat mnoha způsoby. Někteří lidé mají raději tvar
y = A⋅x + B,
jiní zase tvar
Ax + By = C.
Protože jsou všechny tvary ekvivalentní a je snadné mezi nimi přecházet,
není problém dostat tvar, kterému dáváte přednost. Ten poslední je populární
také proto, že přímo dává normálový vektor k dané přímce, následně i směrový
vektor. Tyto vektory jsou užitečné při zkoumání geometrie. Jak je dostaneme?
Pokud známe směrnici k nějaké přímky, pak je její směrový vektor
roven B = (1,k). To mimo jiné znamená,
že když máme funkci f a bod a, pak
v = (1,f ′(a)) je tečný
vektor ke grafu f v a. Máme dva užitečné speciální případy:
Tečný vektor k implicitní křivce
F(x,y) = C se dá
také najít jako
v = (dF/dy,−dF/dx).
Tečný vektor k parametrické křivce
x = x(t),
y = y(t) se dá také najít
jako
v = (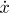 ,
,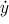 ).
).
Když máme tečný vektor (u,v), dostaneme normálový
vektor snadno jako (v,−u).
"Related rates"
Zpět na Teorie - Aplikace
![]()
![]()
![]() ,
,![]() ).
).