Taylorův polynom

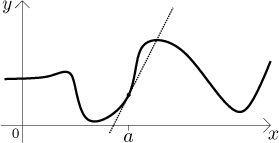
V předchozí sekci jsme mluvili o aproximaci funkcí tečnami. To je samozřejmě užitečné, ale byl tam drobný problém. Uvažujme následující obrázek.

Tečna tam sice aproximuje funkci docela pěkně blízko a, ale chyba rychle roste, když se trochu vzdálíme. Důvod je jasný, funkce se kroutí a tečna ne. Rozhodně bychom dostali lepší výsledky, kdybychom zkusili aproximovat pomocí nějaké funkce, která se také kroutí. Druhá nejjednodušší (po přímce) je kvadratický polynom, který dává parabolu. Opravdu se z obrázku zdá, že bychom s parabolou dokázali víc:

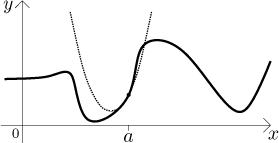
Jak najdeme parabolu, která nejlépe pasuje? Na to se musíme podívat blíže na požadavky na tečnu. Měli jsme dva. První byl, aby tečna procházela daným bodem. Druhý pak byl, aby se "tiskla" ke křivce, jinými slovy aby měla v bodě a stejný směr jako funkce. Chtěli jsme tedy, aby tečna a funkce měly stejnou hodnotu i derivaci v bodě a. Pak jsme dostali vzorec tečny, teď jej trochu přeorganizujeme, aby se nám lépe hodil.

Abychom dostali nejlépe padnoucí parabolu, tak evidentně budeme chtít oba tyto požadavky a přidáme další, má smysl žádat, aby se parabola kroutila v a stejně jako f, tedy chceme také rovnost druhých derivací. Trocha analýzy ukáže, že parabola splňující tyto tři požadavky je dána vzorcem

Parabola aproximovala lépe, ale z obrázku je jasné, že kubická křivka by zabrala ještě lépe a přitom to moc nezkomplikuje, s polynomy se dobře pracuje.

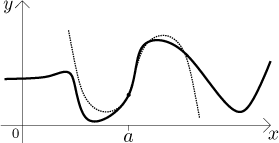
Nejlépe pasující kubická křivka splňuje stejné podmínky jako parabola a navíc má stejnou třetí derivaci v a jako f, je dána

Většina toho, jak se vzorec tvoří, je už asi jasná. Samozžejmě není důvod se zastavit u trojky, polynomy jsou úžasné funkce a můžeme zvyšovat stupeň aproximujícího polynomu, dokud nebudeme spokojeni.

Definice.
Nechť funkce f má všechny derivace až po řád n v a. Pak definujeme Taylorův polynom f stupně n se středem a jako

Všimněte si, že i první dva členy vlastně následují stejný vzorec s derivací a faktoriálem, který máme v sumě, například f (a) se dá zapsat jako [f ⁽⁰⁾(a)/0!]⋅(x − a)⁰.

Věta.
Nechť má funkce f všechny derivace až po stupeň n v a, nechť T je Taylorův polynom f stupně n se středem a. Pak T splňuje

T(a) = f (a),   T ′(a) = f ′(a),   T ′′(a) = f ′′(a), . . . , T ⁽ⁿ⁾(a) = f ⁽ⁿ⁾(a),

a je to jediný polynom stupně nejvýše n s touto vlastností.

Řekněme, že chceme aproximovat funkci f polynomem p (pro několik možných důvodů viz níže). Jak už jsme viděli, podmínky p(a) = f (a), p ′(a) = f ′(a), p ′′(a) = f ′′(a) atd. pak jsou přirozené. Obecný polynom stupně n má n + 1 neznámých koeficientů, ony rovnosti výše nám zase dodají n + 1 rovnic. To znamená, že můžeme vyřešit a najít neznámé koeficienty, dostaneme tak přesně ty, které jsou v definici Taylorova polynomu.

Příklad: Uvažujme funkci f (x) = . Najděte její Taylorův polynom stupně dva v a = 4. Použijte jej k odhadu druhé odmocniny z 5.

Řešení: Abychom mohli vytvořit T₂, potřebujeme první dvě derivace f, pak do nich musíme dosadit a.

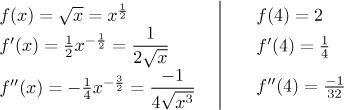
Teď vytvoříme příslušný Taylorův polynom.

Zbyývá odhadnout odmocninu z 5.

Všimněte si, že jsme onen Taylorův polynom neroznásobovali. Je tradice nechávat Taylorův polynom v tomto tvaru, protože pak hned vidíme, jaký je referenční bod a pro tento Taylorův polynom. Všimněte si, že se a nikde jinde ve značení neobjevuje. Některým autorům se to nelíbí a používají značení T_a,n. My jsme se rozhodli následovat druhou zvyklost, protože je to jednodušší, a jak jsme viděli, střed je z polynomu stejně zjevný, pokud jej necháme ve správném tvaru.

Je ještě další důvod, proč v polynomu nechávat členy (x − a). Všechno, co děláme, se nějak vztahuje ke středu a. Když do Taylorova polynomu dosazujeme nějaké číslo x, tak toto číslo x jako takové moc neznamená. Mnohem důležitější je, jak daleko je x od a, mimo jiné to ovlivňuje kvalitu aproximace. To nás přivádí k otázce na chybu aproximace.

Definice.
Nechť má funkce f všechny derivace až do řádu n v a. Uvažujme Taylorův polynom T funkce f stupně n se středem a. Definujeme zbytek jako

R_n(x) = f (x) − T_n(x).

Máme větu, která tento zbytek určuje. Formulace bude trochu neobvyklá, protože obecně nevíme, jestli je x menší nebo větší než a.

První výsledek se jmenuje integrální tvar zbytku, ten druhý se jmenuje Lagrangeův tvar zbytku. Popravdě řečeno, ani tyto dva výsledky nejsou zas až tak užitečné, protože se klidně může stát, že ten integrál je příliš komplikovaný na to, aby šel spočítat, zatímco druhé tvrzení je existenční, víme, že takové c existuje, ale nemáme potuchy, které číslo to vlastně je. Můžeme nicméně odhadnout Lagrangeův tvar shora a s trochou štěstí se tento horní odhad už ukáže jako malý. Vrátíme se k příkladu.

Příklad: Odhadněte chybu, kterou jsme předtím udělali při aproximaci odmocniny z 5.

Řešení: K aproximaci jsme použili T₂, potřebujeme tedy odhadnout zbytek R₂(5). Podle Lagrangeova tvaru existuje c mezi 4 a 5 takové, že

Při odhadu f ′′′(c) shora jsme použili fakt, že c je z intervalu (4,5), tedy c > 4. Vidíme, že chyba, kterou jsme udělali při aproximaci odmocniny z 5 číslem T₂(5), byla nanejvýš 1/512 = 0,002... Můžeme tedy psát

Pro mnoho pěkných funkcí to maximum neroste moc rychle, takže když se vydělí faktoriálem, půjde k nule pro n→∞. To znamená, že pro dané x můžeme dostat libovolně přesnou aproximaci pomocí Taylorova polynomu, stačí vzít dostatečně vysoký stupeň (jinými slovy dostatečně dlouhý polynom). Například všechny derivace sinu a kosinu jsou omezeny jedničkou, takže tyto dvě funkce jdou dobře aproximovat Taylorovými polynomy. Také exponenciála e^x (viz tato poznámka) a logaritmus (viz tato poznámka) mají pěkné aproximace.

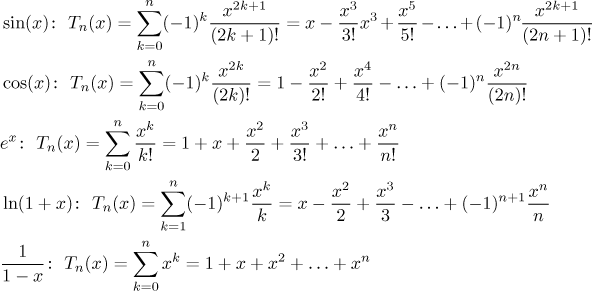
Jak tyto polynomy ukazují, nejčastěji bereme a = 0, protože pak dostaneme pěkné jednoduché mocniny. Takové Taylorovy polynomy jsou tak užitečné, že dokonce mají své jméno, říká se jim Maclaurinovy polynomy. Někdy jsou ale pěkné i jiné středy, například pro logaritmus občas používáme a = 1:

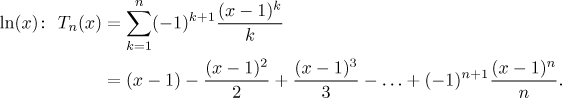
Abychom naznačili, jak to funguje, ukážeme teď několik prvních Taylorových polynomů pro sinus a kosinus. Všimněte si, že polynomy pro sinus v sobě nemají sudé mocniny. To není náhoda, liché funkce mají vždy Taylorovy polynomy jen s lichými mocninami. Díky tomu je také T₂ stejné jako T₁, T₄ je stejné jako T₃ atd., takže nepotřebujeme kreslit Taylorovy polynomy sudého stupně. Podobně budeme kreslit polynomy jen sudého stupně pro kosinus. Všimněte si, jak zvyšováním stupně zvětšujeme množinu, kde je aproximace dost dobrá.

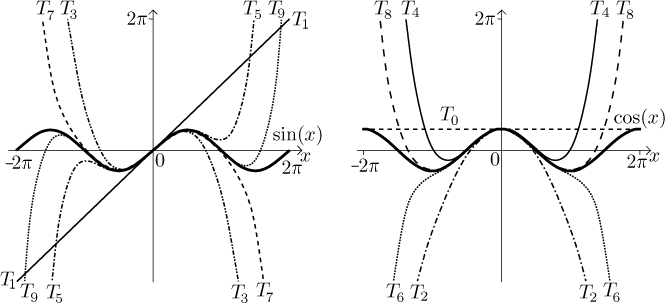
Dobrou aproximaci dokážeme dostat i pro velmi velké části sinu a kosinu tak, že bereme Taylorovy polynomy dostatečně vysokých stupňů. Podobně to funguje u exponenciály. Bylo by ale chybou si myslet, že to je nějaké pravidlo a dá se na to spoléhat. V následujícím obrázku ukážeme prvních několik polynomů pro ln(x + 1).

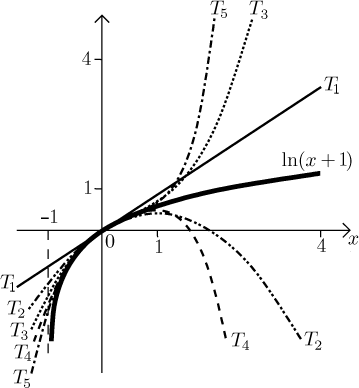
Zde se zdá, že se kvalita aproximace zlepšuje na intervalu (−1,1), ale pro x > 1 to vypadá dost špatně, jako kdyby se polynomy pro vyšší stupeň dokonce od toho logaritmu vzdalovaly. A to je také pravda, v sekci o Taylorových řadách v části Řady - Teorie - Řady funkcí dokážeme, že ty Taylorovy polynomy jsou užitečné coby aproximace logaritmu jen na (−1,1⟩.

Pro stručný přehled a pár dalších příkladů viz Taylorův polynom v části Přehled metod - Aplikace, příklady jsou i v Řešených příkladech - Aplikace.

Abychom náš výklad nějak pěkně uzavřeli, uvedeme formální tvrzení o sudých/lichých funkcích, jak jsme už na to narazili výše.

Proč mluvíme o aproximaci? S funkcemi s komplikovanějšími vzorci se obtížněji pracuje a často je možné je aproximovat něčím hezčím, aniž bychom něco ztratili. Funkce se tak například dají někdy nahradit aproximujícími polynomy v limitách nebo integrálech. Taylorovy polynomy jsou určitě důležité v teoretických úvahách, ale že jsou třeba je asi nejevidentnější v situaci, kdy počítáme něco konkrétního.

My lidé dokážeme dělat pouze čtyři operace, jmenovitě sčítání, odčítání, násobení a dělení. Jak tedy víme, kolik je řekněme sin(2)? A co takhle ln(3), e^1.5, 3^0.13 nebo odmocnina z 5? Tato čísla nelze přesně spočítat pomocí oněch čtyř algebraických operací, ale lidé takové věci potřebovali už stovky let. Nabízí se nápad nahradit tyto nespočítatelné funkce vzorci, které používají pouze ony čtyři operace, které umíme, neboli polynomy. To nelze udělat úplně přesně, což ale není takový problém, protože v praxi stejně pracujeme jen v rámci určité (známé) přesnosti. Taylorův polynom je tak způsob, jak spočítat něco, co bychom jinak nemohli. Stovky let seděli lidé zvaní "computers" v místnostech a plnili archy papíru douhými a nudnými výsledky, abychom dostali tabulky hodnot elementárních funkcí. Vědecké (a inženýrské) výpočty tedy byly dlouhé a silně závislé na aproximaci, kompetentní inženýr si jich spoustu pamatoval.

Příchod programovatelných "computerů" (např. kalkulaček) to před běžným uživatelem schoval, problém ale vlastně zůstal stejný, protože počítačový procesor umí jen stejné algebraické operace jako mozek počítače lidského. Když zmáčkenem na kalkulačce čudlík s nápisem "ln", stane se spousta věcí, jmenovitě kalkulačka rychle proběhne aproximačním algoritmem. Taylorovy polynomy jsou dobrý začátek, ale obvykle vyžadují mnoho operací. To je nemilé, a bylo ještě nemilejší v dobách lidských počítačů. Hodně se tedy bádalo nad nalezením "nejrychlejších" (ve smyslu "vyžadujících nejméně operací") aproximací a tyto výsledky se hodily, když lidé začali konstruhovat kalkulačky.

Tuto sekci uzavřeme následujícím pozorováním. Uvažujme funkci f, která má všude všechny derivace, a zvolme pevně bod a. Můžeme tedy sestavit Taylorovy polynomy s tímto středem libovolného stupně. Předpokládejme, že tato funkce je "pěkná" ve smyslu, že pro každé x jde zbytek k nule, jak jsme to právě diskutovali. To znamená, že v x můžeme aproximovat f (x) s libovolnou přesností pomocí těchto Taylorových polynomů, prostě jen vezmeme dostatečně dlouhý polynom. Zdá se, že jsme v pěkné situaci, ale je tu drobný problém. Neexistuje univerzální stupeň polynomu T_n takový, který by dobře fungoval pro všechna x. Čím je x dále od a, tím delší polynom musíme vzít, abychom dostali potřebnou přesnost, a pokud si zvolímu jednu určitou přesnost a začneme posouvat x do nekonečna, pak stupně potřebných polynomů jdou do nekonečna. To je někdy docela vážný problém. Řešení se nabízí samo: Vezmeme "nekonečné polynomy". Existuje vůbec taková věc? Odpověď je kladná, ale je na to potřeba docela dost teorie, dokonce na to máme speciální kapitolu zde v Math Tutoru. Pro "nekonečné polynomy" se podívejte na Taylorovy řady v části Řady - Teorie - Mocninné řady. Také tam povíme víc o aplikaci Taylorových polynomů.

Zpět na Teorie - Aplikace