Základní vlastnosti integrálů: Přehled metod

Zde si shrneme základní vlastnosti integrálů, které se hodí při výpočtech.

Newtonův integrál neboli neurčitý integrál je množina všech primitivních funkcí F k dané funkci f, značíme jej

Newtonův integrál je lineární:

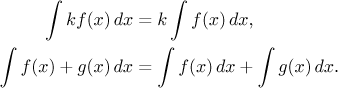
Riemannův (určitý) integrál odpovídá matematickému obsahu oblasti pod grafem f, který je roven geometrickému obsahu částí nad osou x mínus obsah částí pod osou x. Elementární geometrická úvaha pak dává

Také Riemannův integrál je lineární. Jinými slovy se chová rozumný, když vynásobíme integrovanou funkci číslem:

Také si poradí se sčítáním:

Má užitečné srovnávací vlastnosti: Nechť f a g jsou Riemannovsky integrovatelné funkce na ⟨a,b⟩. Jestliže f ≤ g na ⟨a,b⟩, pak