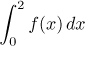 , kde
, kde
Příklad: Vypočtěte
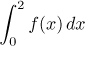 , kde
, kde
![]()
Řešení: Daná funkce vypadá takto:
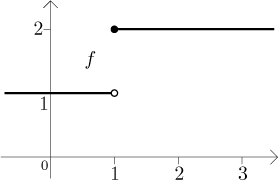
Musíme se rozhodnout, jaká použijeme dělení. Všimněte si, že na obdélnících,
které nezahrnují bod
![]()
Podíváme se na obrázek
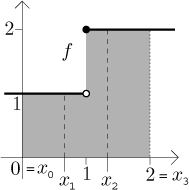
a vidíme, že
![]()
Proto
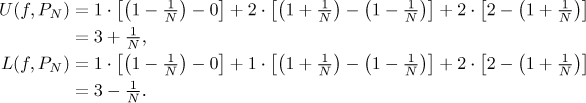
Z obrázku také rovnou vidíme horní a dolní součet, šrafovaná oblast vlevo znázorňuje horní součet, rafovaná oblast vpravo znázorňuje dolní součet:
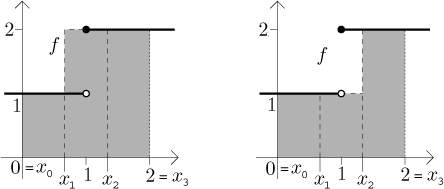
Získáme proto meze pro infimum a supremum
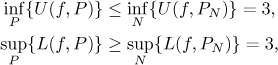
a tak
![]()
Následně
![]()
a
![]()
Tato odpověď se zdá z obrázku jasná, oblast se skládá se tří čtverců o straně jedna.