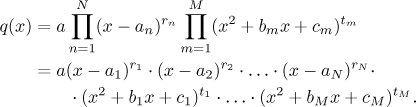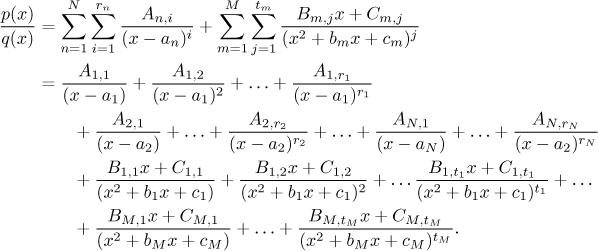Tato metoda se používá při práci s racionálními (lomenými) funkcemi, tedy podíly dvou polynomů. My ji zde samozřejmě využijeme při integrování. Jde o následující tvrzení.
Věta (o rozkladu na parciální zlomky)
Nechť p a q jsou reálné polynomy, nechť stupeň p je menší než stupeň q. Předpokládejme, že q lze rozložit na faktory
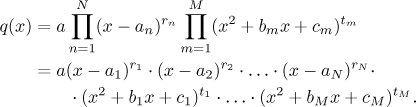
kde jednotlivé faktory jsou navzájem různé a kvadratické členy jsou ireducibilní (nemají reálné kořeny). Pak existuje rozklad
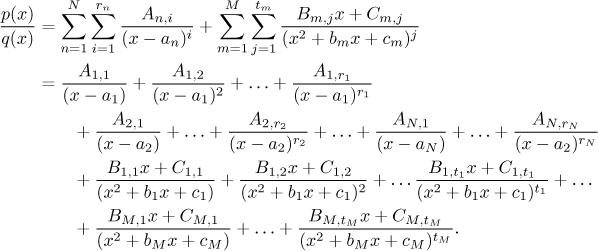
přičemž všechny konstanty A, B a C jsou jednoznačně určeny jmenovatelem příslušného parciálního zlomku.
Co nám to říká? Představme si, že máme dva polynomy
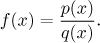
Můžeme předpokládat, že jde o "ryzí" racionální funkci, tedy stupeň čitatele je nižší než stupeň jmenovatele. Věta říká, že problém s třeba i velice komplikovaným podílem se může redukovat na podíly, které jsou znatelně jednodušší a vždy jsou vybírány jen ze dvou typů, tzv. parciální zlomky.
Pro každý lineární faktor
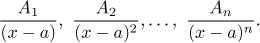
Pro každý ireducibilní kvadratický faktor
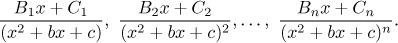
Jako příklad se přesvědčte, že následující rovnost opravdu platí.
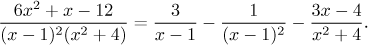
Věta také říká, že rozklad lze udělat jediným možným způsobem. Na druhou stranu nám neříká, jak hledané koeficienty v parciálních zlomcích najít, což není nikterak překvapující, nejsou na to žádné univerzální vzorce. Existuje několik metod, jak tato čísla najít, blíže se tomu věnujeme v sekci o racionálních (lomených) funkcích v části Přehled metod - Metody integrace.
