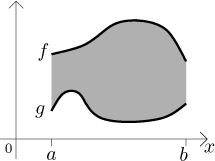
Consider the region bounded from above by the graph of a function f
and from below by the graph of a function g on an interval

If the two functions are Riemann integrable, the area of this region is
![]()
Example: Find the area of the region bounded by
Solution: First draw a picture:
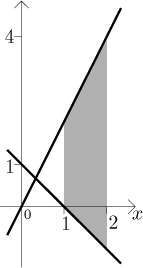
We see that
![]()
If we need to find the area of a more complicated region, we have to decompose it into regions of the above type and add their areas. In particular, this may be necessary when the given functions are intertwined - sometimes one is larger, sometimes the other one.
One good trick that can save work sometimes is the switching of axes. The picture is flipped around the main diagonal, functions change into their inverses and the integral now uses dy.
Example: Find the area of the region below the graph of
Solution: First draw a picture:
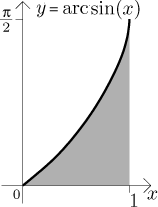
The area is
![]()
This integral is evaluated using integration by parts, which is actually not that bad, but it takes time. The problem becomes easier if we flip the axes:
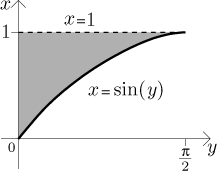
Now the area is easy to find:
![]()
For an explanation how to set up the right integrals intuitively and how to decide whether to switch or not, see the second solved problem. We show there that there are actually two possible approaches to finding the area. One is to remember the above formula and apply it, which may get a bit confusing in more complicated situations. The other approach is to remember the idea behind the formula, that is, the trick with thin stripes, and apply it to a given problem.
Consider a parametric curve
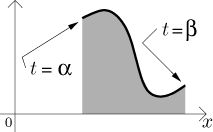
If
![]()
Consider a curve in polar coordinates given by
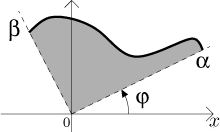
If
![]()