Definice.
Nechť
![]() ak.
ak.
V této sekci uvedeme řady reálných čísel a jejich konvergenci.
Definice.
Nechť{ak}k ≥ n0 je posloupnost (reálných čísel). Pojmem řada (reálných čísel) rozumíme abstraktní symbolak.
Tato definice je trochu divná, protože pořád ještě nevíme, co to řada je. Důvodem pro tento přístup je, že abychom se mohli něco dozvědět o významu tohoto pojmu, musíme nejprve trochu pracovat. Když řekneme "řada", snažíme se tím vyjádřit myšlenku, že máme posloupnost (nekonečnou uspořádanou množinu) reálných čísel a1, a2, a3, atd. (pro zjednodušení teď předpokládáme, že indexy jdou 1, 2, 3,...) a zkoušíme je sečíst:
Tento součet je samozřejmě nekonečný, takže nikdy nekončí a není jasné, co se tím vlastně míní a zda je to vůbec možné. Můžeme my, lidé žijící v konečném světě a konečném čase, vůbec uvažovat o nekonečném sčítání? Necháme tento problém filosofům, kteří se na něm vskutku vyřádili, a uvedeme jeden způsob, jak tuto otázku zodpovědět, a je to způsob, který uspokojuje většinu lidí.
Nejpřirozenější přístup k nekonečným součtům je využít to, co už známe, tedy konečné sčítání. Řečeno jednoduše, začneme sčítat čísla v řadě odleva a postupujeme v ní doprava, přičítáme další a další čísla, a jestliže se průběžné výsledky nakonec usadí u nějaké hodnoty, tak se zdá přirozené prohlásit tuto hodnotu za součet celé řady. Jak se to dělá formálně? Když se podíváme na nekonečný součet reprezentovaný řadou, můžeme z něj udělat součet konečný tím, že uřízneme jeho "ocas" a sečteme jen prvních několik členů.
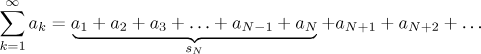
Pro jednoduchost zase předpokládáme, že index začíná jedničkou. Index N představuje bod odříznutí, odpovídající konečný součet se nazývá částečný součet a značí se sN. Je jasné, že toto číslo se liší od celkové nekonečné sumy, ale teď přichází klíčová myšlenka. Vezmeme ten bod odříznutí a začneme jej posunovat doprava, stále počítáme vznikající částečné součty a díváme se, co dělají výsledné sumy. Pokud se blíží k nějaké hodnotě, má smysl tuto hodnotu prohlásit za součet nekonečné řady. Pokud se tyto částečné součty nějaké hodnotě neblíží, pak to ukazuje, že řadu tímto způsobem sečíst nelze. To blížení se znamená limitu.
Definice.
Uvažujme řaduak.
Pro všechna celá čísla N ≥ n0 definujeme její částečné součty vzorcem
Řekneme, že daná řada konverguje (k A), jestliže posloupnost {sN} konverguje (k A). Značíme to
Řekneme, že daná řada diverguje, jestliže posloupnost {sN} diverguje.
Jako obvykle jsou dva speciální případy divergence, které jsou zajímavější. Jestliže jde posloupnost {sN} do nekonečna, pak řekneme, že součet řady je nekonečno a značíme to
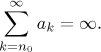
Jestliže jde posloupnost {sN} do mínus nekonečna, pak řekneme, že součet řady je mínus nekonečno a značíme to
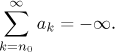
Teď už máme definici, ale není jasné, zda to má nějaký význam, protože představa, že by mohla mít smysl nekonečná suma, je trochu podivná. Existují vůbec nějaké konvergentní řady? Popravdě řečeno, typická řada vybraná náhodně bude divergentní, ale existuje spousta pěkných konvergentních řad. Podíváme se teď na několik příkladů, abychom si ten nový pojem trochu osahali.
Příklad:
Uvažujme řadu
![]()
Toto je triviální případ, dokonce i naprostý řadovní začátečník by si
tipnul, že součet nekonečně mnoha nul by zase měla být nula. Jak to funguje
podle definice? Zkusíme se podívat na prvních pár částečných součtů.
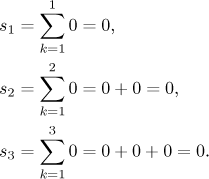
Evidentně sN = 0 pro všechna N, což je posloupnost jdoucí k nule. Podle definice tedy opravdu máme
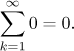
Existují zajímavější příklady konvergentních řad? Zde je jeden, který znali už staří Řekové.
Příklad:
Uvažujme řadu
![]() .
.
Tvrdíme, že tato řada konverguje a její součet je 1. Nejprve zkusíme pomocí
geometrického argumentu ukázat, že to může mít smysl. Podívejte se na
následující obrázek. Začneme s kouskem reálné osy reprezentujícím interval
mezi 0 a 1. Víme, že sčítání čísel se dá reprezentovat na reálné ose tak, že
dáváme úsečky příslušné délky jednu za druhou, a přesně to děláme v našem
obrázku. Nejprve vezmeme úsečku délky
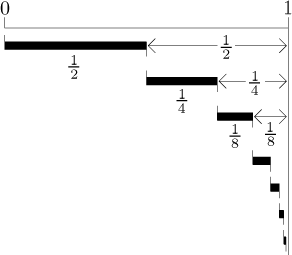
Kolik chybí do 1, což je onen údajný součet celé řady? Evidentně
Mělo by už být jasné, co se děje, v každém kroku doplníme přesně polovnu
toho, co chybí do 1, jinými slovy, v každém kroku pokročíme o polovinu
chybějící vzdálenosti do 1. Celá finta je teď v tom představit si, že když
tohle budeme dělat nekonečně dlouho, dokud nevyužijeme všechna čísla typu
I když tohle může vypadat trochu nereálně, ve skutečnosti se nekonečné sumy sčítají všude kolem nás a reálný svět funguje přesně tak, jak jsme to zde navrhli, stačí se jen dívat na věci správným způsobem. Asi nejúdernější příklad, že ta sumační záležitost je vlastně přirozená, je slavný Zenonův paradox.
Jak to funguje podle definice? V sekci Důležité příklady uvidíme, že částečný součet této řady je
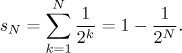
Toto se snadno dokáže indukcí a souhlasí to s naším geometrickým přístupem
výše. Limita
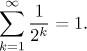
Příklad:
Uvažujme řadu
![]() .
.
Selský rozum naznačuje, že součet nekonečně mnoha 1 by měl být nekonečno. A
opravdu, snadno se nahlédne, že částečné součty jsou
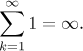
Příklad:
Uvažujme řadu
![]() .
.
Tato řada je zajímavá. Co dostaneme, když začneme sčítat její členy? Začneme
s 1, pak přičteme sousední −1 a dostaneme se se součtem na 0, pak přičteme
1, což posune součet nahoru, ale hned další člen tohle zruší a jsme zpátky
na 0. Jak pokračujeme doprava v naší řadě, celkový součet osciluje mezi 1 a
0. Zdá se tedy, že se součet nikdy neusadí u nějakého čísla, které bychom
pak mohli rozumně nazvat součtem této řady. A to je také pravda. Teď to
zkusíme podle definice.
Už jsme viděli, že výsledek částečného součtu sN závisí na tom, zda je N sudé nebo liché, vzorec je
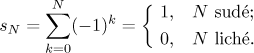
Posloupnost
Poslední dva příklady jsou velmi důležité, protože ukazují, co může způsobit divergenci řady. Jestliže je řada divergentní, pak se buď snaží posčítat příliš mnoho a dojde k nekonečnu (popřípadě sčítá příliš velká čísla se záporným znaménkem a vyjde mínus nekonečno), nebo příliš osciluje; některé řady dokonce zvládnou obojí najednou. Tohle se bude hodit, až se podíváme blíže na problém konvergence v příští sekci a v části Teorie - Testování konvergence.
Poznámka: Existují aplikace, kde je potřeba obecnějšího pojmu
konvergence, mimo jiné taková konvergence, aby také řada z našeho posledního
příkladu konvergovala. Existuje několik takových obecnějších pojmů, jeden
obzvláště užitečný naší poslední řadě určí kompromisní součet
Poznámka: Je jedna pěkná pohádka (Thomsonova lampa), která ukazuje,
jak oscilace může působit problémy, když se snažíme dojít k nějakému
závěru. Co je zajímavé, tento příběh je umožněn faktem, že řada také může
konvergovat. My použijeme řadu z příkladu výše, kde jsme sčítali
Protože víme, že
Někteří lidé mají pocit, že odpověd "není odpověď" stačí, jiní tvrdí, že ten problém má hluboké filozofické důsledky. Například to ukazuje, že i kdybychom měli úplné informace o minulosti nějakého objektu, pak to ještě pořád neznamená, že umíme určit jeho stav právě teď. Co to říká o naší schopnosti poznat náš svět? Jiní zase říkají, že tento příklad není relevantní, protože používá idealizovanou lampu, ve světě skutečném trvá přepnutí vypínače nějaký konečný (a konstantní) čas, tudíž dřív nebo později nebudeme mít čas na přepnutí vypínače požadovanou rychlostí a celá ta věc se sesype. A ještě další míní, že... my jsme naštěstí matematici a zde si s tím nemusíme lámat hlavu.
Všimněte si, že způsob indexování je vlastně irelevantní. Skutečná podstata řady jsou čísla, která do ní jdou. Uvažujme například řadu
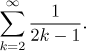
Když ji rozepíšeme v dlouhém značení, dostaneme
![]()
Všimněte si, že dostaneme přesně totéž, když si rozepíšeme
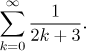
Ony dvě formální řady výše reprezentují tutéž řadu ukázanou mezi nimi, proto musí mít stejné vlastnosti, jde jen o dva rozdílné výrazy pro tentýž objekt. Poučení z tohoto příkladu je, že bychom se neměli příliš upínat na jedno určité vyjádření, ale vždy myslet na to, co ono vyjádření říká. V mnoha případech pomůže našemu porozumění, když si řadu rozepíšeme dlouhým způsobem. Občas dokonce silně pomůže, když si řadu přepíšeme do jiného výrazu. Jak se to dělá? Vždy si můžeme řadu napsat dlouhým způsobem a pak zkusit uhádnout nějaký lepší způsob její indexace, ale většinou dopadneme lépe, pokud použijeme substituci. Základní myšlenka je stejná jako u substituce pro jiné pojmy (limita, integrál atd, viz substituce). Namísto dlouhého vysvětlování ukážeme, jak se přejde od prvního k druhému vyjádření výše.
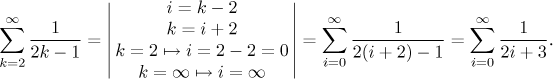
Jako obvykle si nejprve vybereme základní substituční rovnost, v tomto
případě
Posunová substituce neměníme vlastnosti řady.
Fakt.
Jestliže změníme indexaci řady pomocí substitucei = k + a pro nějaké celé číslo a, pak má nová řada přesně stejné vlastnosti jako řada původní.
To znamená, že neuděláme chybu, když budeme uvažovat pouze řady, jejichž
indexy začínají v
Obecnější substituce jsou možné, ale používají se zřídka. Jedním z důvodů je, že musíme dávat velký pozor na zachování pořadí sčítání členů (viz přerovnání v následující sekci) a také musíme hlídat, abychom nějaký člen nevynechali.