Zde dokážeme, že pro každé x je součet |sin(x)| a |sin(x + 1)| roven vždy alespoň sin(1). Za tím účelem budeme uvažovat funkci

f (x) = |sin(x)| + |sin(x + 1)|.

Jaké jsou její extrémní hodnoty? Protože je tato funkce π-periodická, stačí najít její globální extrémy na ⟨0,π⟩. Použijeme standardní postup přes derivace, viz Globální extrémy v části Derivace - Přehled metod - Aplikace. Abychom ale mohli derivovat, musíme se nejprve zbavit absolutní hodnoty. Protože zde bereme x mezi 0 a π, můžeme tu první absolutní hodnotu prostě ignorovat. Druhý člen už ovšem může být jak kladný, tak záporný, kritickou hodnotou je zde π − 1. Máme tedy dva případy.

Případ 1: x je mezi 0 a π − 1. Pak

f (x) = sin(x) + sin(x + 1).
f ′(x) = cos(x) + cos(x + 1).

Kdy je tato derivace rovna nule? Tuto rovnici neumíme řešit analyticky, ale jde to graficky. Podíváme se na první vlnu kosinu a začneme podél ní posouvat úsečku o délce 1, čekáme přitom na chvíli, kdy budou hodnoty na jejích koncích přesně opačné.

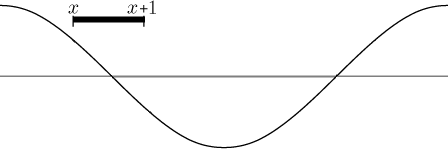
To se stane, když je úsečka symetricky okolo bodu π/2, takže x = π/2 − 1/2. (Druhá taková pozice je okolo bodu 3π/2, ale pak by x bylo mimo naši oblast, tj. větší než π − 1.) Abychom našli globální extrémy na intervalu ⟨0,π − 1⟩, podíváme se na koncové body a kritické body:

•   f (0) = sin(1);
•   f (π/2 − 1/2) = sin(π/2 − 1/2) + sin(π/2 + 1/2) = 2sin(π/2 − 1/2);
•   f (π − 1) =  sin(π − 1) = sin(1).

Všimněte si, že π/2 − 1/2 > 1 a π/2 − 1/2 < π/2, proto je jeho sinus větší než sin(1). Prostřední hodnota je tedy maximum a minimum je sin(1), přesně jak jsme tvrdili. Na prvním intervalu to funguje.

Případ 2: x je mezi π − 1 a π. Pak

f (x) = sin(x) − sin(x + 1).
f ′(x) = cos(x) − cos(x + 1).

Kdy je derivace rovna nule? Teď čekáme na chvíli, kdy jsou hodnoty na koncích úsečky klouzající podél kosinu stejné. Jsou dvě takové pozice, když je úsečka nad počátkem a když je symetricky kolem bodu π. První možnost dává x = −1/2, což je mimo naši oblast, ale ta druhá dává relevantní hodnotu x = π − 1/2. Abychom našli globální extrémy na intervalu ⟨π − 1,π⟩, podíváme se na koncové body a kritické body:

•   f (π − 1) =  sin(π − 1) = sin(1);
•   f (π − 1/2) = sin(π − 1/2) − sin(π + 1/2) = 2sin(1/2);
•   f (π) = −sin(π +  1) = sin(1);

Zase je maximální ta prostřední hondota, což se nahlédne například takto:

2sin(1/2) > 2sin(1/2)cos(1/2) = sin(2⋅1/2) = sin(1).

Zase máme minimum sin(1), přesně jak jsme tvrdili. Když dáme oba případy dohromady, dokázali jsme naše tvrzení.