Zde dokážeme, že pro každé x je alespoň jedno z čísel |sin(x)|, |sin(x + 1)| a |sin(x + 2)| větší než 1/2. Použijeme jednoduchý geometrický důkaz, ve kterém také využijeme fakt, že π/6 je trochu víc než 1/2, proto je π/3 o trochu víc než 1; hodnota π/6 je tu evidentně zásadní, protože je v ní sinus roven 1/2.

Důkaz uděláme tak, že probereme všechny možné situace. Jestliže je |sin(x)| > 1/2, tak jsme hotovi. Předpokládejme tedy, že to není pravda. Pak musí být x mezi nπ − π/6 a nπ + π/6 pro nějaké celé číslo n (viz obrázek níže).

Jestliže je x v pravé polovině tohoto intervalu, pak x + 1 musí být větší než nπ + π/6 (neboť π/6 < 1), ale menší než nπ + 5π/6, takže |sin(x + 1)| > 1/2 a jsme hotovi.

Poslední případ tedy je, když x leží v levé polovině, to jest mezi nπ − π/6 a nπ.

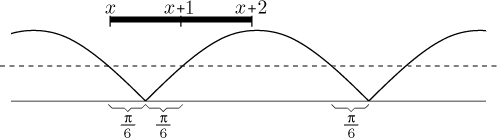
Pak musí být číslo x + 2 zase větší než nπ + π/6 (neboť π/3 < 2), ale menší než nπ + 5π/6, takže |sin(x + 2)| > 1/2. Protože to byl ten poslední zbývající případ, pokryli jsme všechny možnosti a vždy našli jednu velkou hodnotu, přesně jak jsme potřebovali.