Rovnice vedení tepla je jednou ze tří základních parciálních diferenciálních rovnic. Popisuje, jak se pohybuje teplo. Použijeme teď elementární analýzu z prvního semestru, abychom ji v jednoduché situaci uhádli.
Představte si, že máte ocelovou tyč. Má nějaké počáteční rozdělení teploty, například jsme náš experiment mohli začít tak, že jsme tuto tyč vytáhli z mražáku a velice rychle rozpálili jeden konec plamenem. Pak plamen zastavíme a budeme sledovat, co na různých místech tyče dělá teplota. Základní princip je, že se teplo pohybuje z míst, kde je ho hodně, do míst, kde je ho méně.
Nejprve si musíme upřesnit situaci. Pro jednoduchost budeme předpokládat, že
tyč je tak tenká, že má vždy stejnou teplotu na celém řezu, takže se teplota
mění, jen když se pohybujeme podél tyče. K popisu teploty tyče nám tedy
stačí vzít funkci
Potřebujeme ještě jeden zjednodušující předpoklad, budeme předpokládat, že si tato tyč nevyměňuje teplo se svým okolím, například protože je izolovaná. Nebudeme si také dělat starosti s jejími konci.
Teď už jsme připraveni přemýšlet nad tou správnou rovnicí. Jako obvykle je nejlepším výchozím bodem otázka na změnu a co ji způsobuje. Proto si zvolíme pevně nějaký čas t a pozici x na tyči. Toto bude "naše" místo. Zajímá nás rychlost změny teploty v tomto čase a na tomto místě. V této chvíli máme určitou teplotu, co by "nás" přinutilo ji změnit?
Protože předpokládáme nulovou výměnu tepla s okolím tyče, tak jediným relevantním faktorem je teplota sousedících částí tyče. Je jasné, že pokud mají sousední části napravo a nalevo stejnou teplotu jako "my", pak nemáme důvod něco měnit. Podobně nemáme důvod pro změnu, jestliže je na jedné straně tyče tepleji, ale na druhé straně je o přesně tentýž rozdíl chladněji.
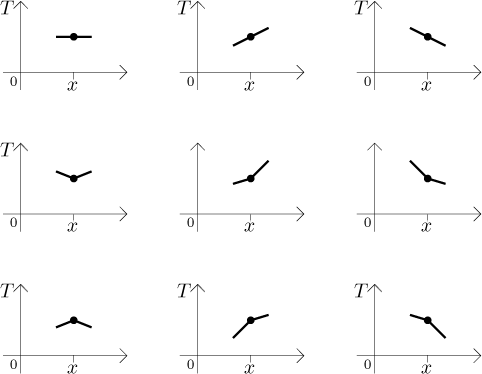
"Naši" teplotu tedy změníme jen tehdy, pokud je mezi přilehlými částmi nějaká nerovnováha. Čím větší nerovnováha, tím větší změna teploty - to zní logicky. Jak se to vyjádří matematicky? Ten správný nápad dostaneme, když se podíváme na pár obrázků. Ukážeme teď jednoduché grafy teploty na tyči pro náš čas (na chvíli jej zmrazíme). V prvním řádku je několik příkladů distribuce teploty kolem nás, kdy nemáme důvod tu naši měnit. V druhé řadě jsou příklady, kdy naši teplotu chceme zvýšit, ve třetí řadě pak teplotu chceme snížit.

Když se na ty tvary podíváte, měli byste okamžitě pomyslet na konvexitu. Jak se konvexita funkce zjistí? Používáme na to druhou derivaci, zde potřebujeme derivovat dvakrát vzhledem k pozici na tyči, tedy vzhledem k x. Jak to tedy funguje? Chceme naši teplotu zvýšit (tedy derivace T vzhledem k času by měla být kladná), jestliže T bráno jen jako funkce x je konvexní, tedy když je druhá derivace T vzhledem k x kladná. To naznačuje přímou závislost a my uhádneme následující rovnici:
![]()
Náš závěr má jeden závažný problém. Jak jsme věděli, že je ta závislost lineární? Co když časová derivace závisí řekněme na třetí mocnině druhé prosorové derivace? Nebo je tam ještě jiná závislost? To je přesně chvíle, kdy končí naše hádání a začíná vážná fyzika (nebo experimenty potvrdíme, že jsme se trefili), každopádně ta rovnice je dobře. Ve více rozměrech (když pracujeme s objemem namísto s délkou a tudíž máme víc prostorových proměnných x1, x2,...) to vypadá takto:
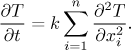
Tato rovnice vedení tepla je základem pro všechny situace týkající se tepla; věci jako žádná/částečná/plná izolace, vnější zdroje tepla, různá chování na povrchu tělesa a další faktory ji jen modifikují, jádro zůstává stejné. O řešení této rovnice v různých situacích byly napsány tlusté knihy, v komplikovnějších podmínkách pak používáme numerické aproximace na počítačích, které sdílejí mnoho myšlenek s aproximačními fintami použitými v předchozí sekci.
Jaký měl tento příklad smysl? Asi tak, pokud jste se podívali na ty obrázky nahoře a napadla vás konvexita, tak jste si sami vyzkoušeli hlavní smysl matematiky - pomoci nám při zapisování našich nápadů (a pak s trochou štěstí i nabídnout nějaké řešení).