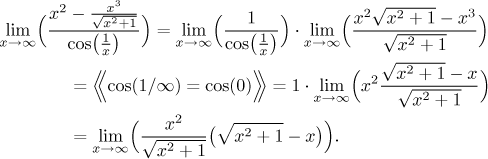
7: The term with square root is the most interesting one, because on this type one can use intuitive calculations. When x grows to infinity, the "+1" under the root can be ignored, so the root is essentially taken from x², which gives x; this in turn cancels with the x in the numerator. Thus the fraction gives 1 and the whole bracket goes to 2. Therefore it will be better to evaluate it separately, the intuitive calculations can be done properly by factoring out leading powers.

Similarly, the cosine part can be figured out by substituting in infinity and using the limit algebra. What is left is the x² and the sine in the denominator, since they together form the indeterminate product. However, now it is easier than it was before, especially if you notice that one can pull the square out of the limit. Try it, then change the product into a ratio.

Remark: If you tried the direct l'Hospital, your best bet is to get here:

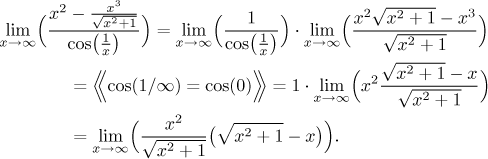
Intuitive calculations show that the fraction is about x when x grows large and we also know that it can be easily figured out by factoring. However, since it tends to infinity, it cannot be handled separately from the second term, because that one could be zero and there would be trouble. Actually, you did investigate exactly this before and you did get zero. Now you need to put the infinity and the zero parts together and somehow compare and/or cancel.

The best way seems to be to use the result from the beginning, when the difference was investigated and the root was removed using algebra. Why? All the terms in play are some powers and roots, so hopefully - after getting rid of the indeterminate difference - they can be put together and handled like any other ratio of polynomials and powers.

Next hint
Answer