21: You should get

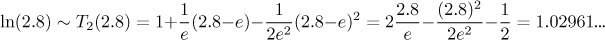
The Lagrange estimate of the error is

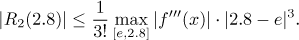
Determine the maximum in the formula.

Next hint
Answer

Remark: This example may look a bit funny if this approximation is understood as a way to avoid using computers and/or calculators, since the above estimate could not be done reasonably with just a paper and pencil (unlike other problems here). However, the main use of approximation today is different. The number ln(2.8) cannot be calculated using algebraic operations. Thus it is not possible to get this number precisely using computers. On the other hand, once we have e stored in memory, we can evaluate the approximating expression above using only algebraic operations, which means that a computer can do it.

One may try to get around this by taking the center a = 1. Then the resulting polynomial and also the approximating expression only features "nice" numbers. However, the Lagrange estimate of error is then rather huge (which may not mean much, since it is just an upper estimate and it may exaggerate). Unfortunately, the error is in fact very huge and more advanced theory shows that by increasing the degree of Taylor's polynomial we increase this error still more! The Taylor approximation of logarithm with center a = 1 works well only for x < 2, so this is a dead end.