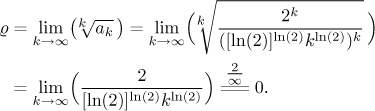
22: Odmocninové kritérium vede na
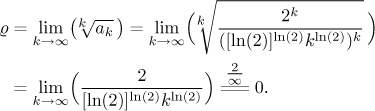
Protože je tato konstanta menší než 1, zkoumaná řada a proto také i daná řada konverguje.
Limita z Jermakovova kritéria se dá udělat relativně snadno s pomocí výpočtu, který byl udělán dříve pro odmocninové kritérium, když bylo aplikováno na danou řadu.
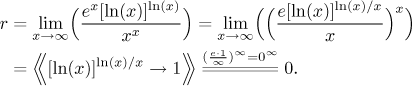
Jsou další alternativy. Víme například, že logaritmy rostou pomaleji než
mocniny, takže také
![]()
Nebo se dá všechno převést na exponenciály
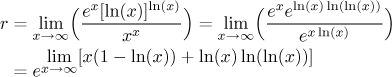
a pak ukázat, že ten výraz v exponentu jde do mínus nekonečna, je prostě docela dost způsobů, jak se k výsledku dostat.
Každopádně je r menší než 1, což potvrzuje konvergenci dané řady.