If you wish to simultaneously follow another text on sequences in a separate window, click here for Theory and here for Solved Problems.
There are two important properties one can ask about (other than the property - convergence): boundedness and monotonicity.
The easiest way to check on boundedness of a sequence is to look at the
expression
There is no algorithm for finding such a h, all depends on experience.
Boundedness from below or from above is done similarly, one uses experience
to decide whether the appropriate inequalities
Example: Explore the boundedness of the sequence
![]() .
.
Solution: First we attempt to prove boundedness. Is there a number
h so that for all n natural one has
The function defining our sequence is a quadratic polynomial whose graph is a
parabola, in this case a parabola going up. Since we are considering natural
numbers that go to infinity, from the graph it seems that the values will
also increase beyond any bound. Thus the given sequence is not bounded.
However, we know that such a parabola does not extend down indefinitely. In
fact, it is easy to show that its vertex has coordinates
Again, here there is no definite algorithm for determining monotonicity. The standard procedure is as follows.
In case the sequence is given by a function, it is possible to investigate the monotonicity of the function and with a bit of luck we get the answer and also a proof (cf. Sequences and functions in Theory - Limits).
Example: Investigate monotonicity of the sequence
![]() .
.
Solution: We calculate the first few terms:
We want to show that for all natural numbers n, the inequality
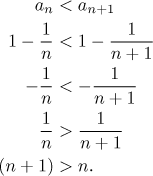
The operations were equivalent and the last line is obviously true, hence so is the first one and the proof is finished.
Alternative solution: The sequence is given by the function
Two more solved examples of sequences investigated for boundedness and monotonicity can be found in Solved Problems - Basic properties.