Problem: Investigate boundedness and monotonicity of

Solution: We try to calculate the first few terms: a₁ = 3 + sin(1), a₂ = 6 + sin(2)/2, a₃ = 9 + sin(3)/3, a₄ = 12 + sin(4)/4. How large are these numbers? Since |sin(n)| ≤ 1, the second part in addition is always at most 1 in absolute value. The first seems to increase by 3, so the next term in the sequence is always larger than the previous one by a number between 1 and 5. Why? We have a₁ = 3 ± 1, a₂ = 6 ± 1, a₃ = 9 ± 1, a₄ = 12 ± 1, and so on. (In fact, we have for instance a₄ = 12 ± 1/4, but the easier though less precise estimate is enough.) What does it suggest? First, the sequence probably tends to infinity, therefore it is not bounded. However, it is probably bounded from below. Second, as we saw, the sine term is small compared to the increase by 3 at every step, so this sequence is probably increasing.

Proof of boundedness from below:
We always have 3n² + sin(n) ≥ 3n²−1 ≥ 0 for natural numbers n, which proves that the sequence satisfies a_n ≥ 0; that is, the sequence is bounded from below.

Now we will show that this sequence tends to infinity, hence it cannot be bounded from above, consequently it is also not bounded. We will prove it by comparison, see for instance Methods Survey - Limits - Comparison and oscillation.

Proof of monotonicity: We will test the inequality for an increasing sequence.

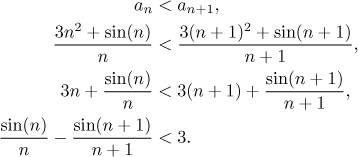
Is this inequality true? Now it is not so clear, but let's see: The sine is always at most 1, so we can estimate

Thus the last inequality above was true, therefore also the first one. We proved that the given sequence is increasing.

Could we use methods from function calculus? We can try. We will investigate the function 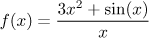(see Theory - Limits - Sequences and functions). We find the derivative:

Just like before, from boundedness of sine and cosine by 1 we conclude that the derivative is at least 1 for x ≥ 1. In particular, the derivative is positive, which means that f is increasing on (0,∞). Consequently, the given sequence is increasing.

Remark: An experienced problem solver would prefer to work with the expression

a_n = 3n + sin(n)/n,

calculations are then a bit easier (the derivative by quite a bit).

Back to Solved Problems - Basic properties