Algebra of limits (with infinity)

What follows is a list of algebra expressions that can be used for calculating limits. It is an extension of the usual algebra. We also mention indeterminate expressions here. They are dealt with in more detail here. Be sure to look at Notes at the end for proper understanding of the rules, especially at the very last note. Here you find a brief list of the limit algebra if you want just a summary.

Addition/subtraction:
Real numbers add/subtract in the usual way.
Infinity behaves nicely in most cases:
∞ ± L = ∞ for all real L,
∞ + ∞ = ∞.
Indeterminate expression: ∞ − ∞.

Multiplication/division:
Real numbers multiply in the usual way, also division works as usual as long as the denominator is not equal to zero.
1/0⁺ = ∞ and 1/0^- = −∞, where 0⁺ stands for a sequence tending to zero whose terms are all positive and 0^- stands for a sequence tending to zero whose terms are all negative (in fact, it is enough to have the positivity/negativity valid only at the "end" of the given sequence, that is, after dropping its "beginning", a finite number of terms). See the note at the end.
Infinity behaves nicely in the following cases:
∞⋅L = ∞ and ∞/L = ∞ for all positive L,
∞⋅L = −∞ and ∞/L = −∞ for all negative L,
L/∞ = 0 for all real L,
∞⋅∞ = ∞.
Indeterminate expressions: ∞⋅0, 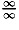, and .
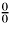The expressions L/0 for L not zero and ∞/0 are usually not included among indeterminate expressions, but they do belong there, since they can yield three distinct answers: ∞, −∞ and "DNE" (Does Not Exist). For details see Notes below.

Powers:
Real numbers work in powers in the usual way; in particular, the power A^B works as usual for positive A. When A is not positive, one has to be cautious, in particular 0⁰ is an indeterminate expression (see below).
Infinity behaves nicely in the following cases:
∞^L = ∞ for all positive L, ∞^L = 0 for all negative L,
L^∞ = ∞ if L > 1, L^∞ = 0 if |L| < 1, and L^∞ DNE if L < −1,
L^−∞ = 1/L^∞ = (1/L)^∞, so L^−∞ = 0 if |L| > 1, L^−∞ = ∞ if 0 < L < 1, and L^−∞ DNE if −1 < L < 0.
∞^∞ = ∞.
Indeterminate expressions: 1^∞, 0⁰, ∞⁰.

Some elementary functions:
e^∞ = ∞, therefore e^−∞ = 1/e^∞ = 1/∞ = 0.
ln(∞) = ∞ and ln(0⁺) = −∞, where 0⁺ stands for a sequence tending to zero whose terms are all positive (or at least they are positive if the first few are dropped).
arctan(∞) = π/2, arctan(−∞) = −π/2.

Notes

In the above equalities any given symbol does not stand for an actual number; rather, it symbolizes sequences whose limit is equal to this specific symbol. For instance, 2⋅3 = 6 in this context does not refer to real numbers, but it reads: "When a sequence converging to 2 is multiplied by a sequence converging to 3, the resulting sequence converges to 6." This explains why the limit algebra sometimes fails in examples that would seem obvious if we were dealing with numbers. For instance, one to any power is one, but one to infinity is an indeterminate expression! Why?

One to infinity is in fact a shortcut for a sequence that converges to 1 raised to a sequence that converges to infinity. Since we perform the operation term by term, we obtain the sequence of powers {a_n ^b_n}, where the bases a_n are eventually close to 1, but they need not be exactly one. For instance, they might all be slightly more than one. Since they are raised to huge numbers (the exponents b_n tend to infinity), they may yield big answers and the resulting sequence may even converge to infinity. It all depends on balance. If the exponents become really big before the bases have a chance to get close to 1, then "one to infinity" may be a big number. On the other hand, if the bases get really close to 1 really fast, while exponents are growing to infinity slowly, then the closeness of bases to 1 may outweight the growth of exponents and "one to infinity" could be close to one.
Similarly, if the bases are less than one and tend to one slowly, while exponents get big really fast, then "one to infinity" may be small, even zero.

Similar balance decides the outcome of other indeterminate expressions, for instance the outcome of ∞ − ∞ depends on which of the infinities becomes large faster.

It is enough to investigate 1/0, since expressions L/0 and infinity divided by zero behave in exactly the same way. The basic idea is that one divided by a really tiny number is a really huge number whose sign depends on the sign of the divisor. Since with a tiny number it is just a small change from positive to negative, it follows that such a small change in the denominator will make a huge change in the outcome: the large number changes sign (for instance, 1/0.0001 = 10,000, while 1/-0.0001 = −10,000).

Recall that "0" stands for some sequence {a_n} that tends to zero. The outcome of 1/0 depends on the signs of a_n. If all a_n are positive (this is denoted by 0⁺ in the limit algebra, it is actually enough if the terms become positive after the first few are dropped), it follows that we always divide "almost one" (recall that "1" stands for some sequence b_n tending to 1) by a small positive number, obtaining a huge positive answer. Therefore the resulting limit should be infinity. On the other hand, if all a_n are negative (this is denoted by 0^- in the limit algebra, it is actually enough if the terms become negative after the first few are dropped), it follows that we always divide "almost one" by a tiny negative number, obtaining a negative number that in absolute value is very huge. Therefore the resulting limit should be negative infinity. In this way we obtain the two formulas for 1/0 in the limit algebra above: 1/0⁺ = ∞ and 1/0^- = −∞.

The third alternative is that as we follow the sequence a_n towards its end, no sign prevails; that is, no matter how far we go along the sequence, there are always negative and positive a_n further on. This can be also expressed like this: It is not possible to make the sequence have the same sign by ignoring its beginning, that is, by dropping a finite number of its terms. Since the sequence a_n tends to zero and b_n is about one for large n, the numbers b_n /a_n in absolute value grow to infinity, but the signs keep changing from plus to minus and back in some way; thus b_n /a_n yields an oscillating sequence, with the size of oscillation growing. In such a case the outcome is that the limit of the sequence b_n /a_n does not exist.

The conclusion is that when we see the type 1/0, we have to investigate the sign of the sequence in the denominator. If we find out that a certain sign eventually prevails, we can use the limit algebra. If we find that no sign prevails, they keep changing, the answer is that the limit DNE. If we are unable to investigate the signs, then we have to give up on this particular case of 1/0.

For some examples of this behaviour, see indeterminate expressions.

In this note we put together the two ideas from the previous notes to explain why sometimes we need to consider one-sided limits.
The fact that a number in limit algebra is not exactly this number, but a symbol for a convergent sequence, allows us to do things which could not be done with numbers. For instance, we know that we cannot substitute the number 0 to the function 1/x². However, in the limit algebra we have 1/0² = ∞ (almost, as we will explain). Why? 0 stands for a sequence {a_n} that converges to zero. If this sequence satisfies the condition that a_n are different from zero, then a_n² are positive numbers converging to zero, so 1/a_n² must go to infinity. We can actually write 0² = 0⁺ and use the result from the previous note.

Sometimes when we try to substitute a number representing a convergent sequence into a function, we have to be careful and do extra work. For instance, what is the outcome of ln(0)? Recall that logarithm is defined only for positive numbers, so here one has to look closely at the sequence {a_n} represented by "0". In order to make sense, its terms have to satisfy a_n > 0. Then they can be substituted into logarithm and ln(a_n) goes to −∞.

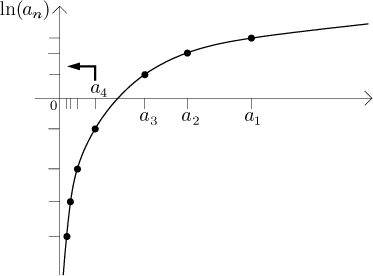
We marked the sequence on the real line, the values of ln(a_n) appear on the vertical axis.

We had a notation for such "0", in the previous note we called it 0⁺, and we just argued that ln(0⁺) = −∞.

These considerations are used quite often and deserve a formal definition.

Definition (one-sided limits)
Let {a_n} be a sequence that converges to a real number A.
If a_n > A for all n, we say that {a_n} converges to A from the right. We denote it a_n→A⁺, and in the limit algebra we would use the symbol A⁺ for such a sequence.
If a_n < A for all n, we say that {a_n} converges to A from the left. We denote it a_n→A^-, and in the limit algebra we would use the symbol A^- for such a sequence.

In the following pictures we show how one-sided limits look like.

We saw two most typical examples when one-sided limits are useful, expressions 1/0 and ln(0). In fact, whenever you get these two expressions, you do have to investigate whether the 0 is one-sided, otherwise you cannot make any conclusion regarding the outcome. There are more examples like this. Every time you are trying to substitute some A into a function and you run into trouble, you should ask whether the situation could be helped if A is of the one-sided type.

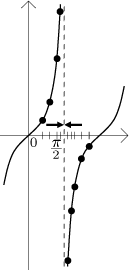
Example: What is the outcome of tan(π/2)?

We know that tangent is not defined at π/2, which shows that we should investigate further. Since we know how tangent looks like,

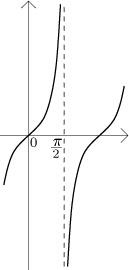
we see that this is exactly the situation where one-sided limits can help. If we imagine examples of sequences tending to π/2 from the right and from the left,

we should be able to make the correct guess:

tan((π/2)⁺) = −∞,      tan((π/2)^-) = ∞.

So when faced with tan(π/2), the sequence inside tangent has to be investigated in more detail. If the limit is one-sided, the outcome is as above. If the sequence keeps jumping to the right and left of π/2, the limit does not exist.