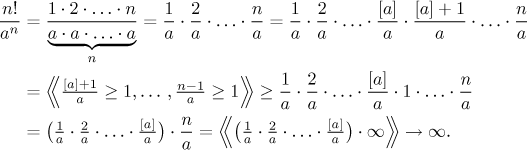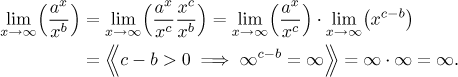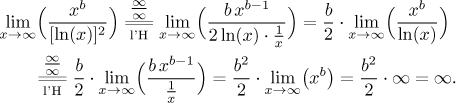Order of infinity
When talking about different "sizes" of infinity, we are actually talking
about "order". It is a mathematical notion of comparing how large or small
functions are at a given point. Since we only need it for sequences, we will
not do a complete exposition in full generality here and we will be less
formal. Hopefully, it will be more understandable this way.
Consider two sequences, an and
bn. We want to compare how they behave when n
gets really large. Typically, both sequences would tend to infinity and we
want to compare the "sizes" of these two infinities, but it is not the only
possibility. We may also compare how the sequences converge to some number.
Typical example is when both converge to zero. We know that 0/0 is an
indeterminate expression, so we may wonder which of the two zeros is "more
zero" and wins. For examples of this, check the 0/0 part of
indeterminate expressions.
We will actually talk about two kinds of comparison. The notion of
order compares infinites roughly; when one expression has a higher
order, it means that it is substantially larger, not just by a little bit.
From another point of view, when two sequences are of the same order at
infinity, they are more or less the same.
This is useful for finding which parts are less important and which terms
prevail over which when it comes to direct confrontation, but it is not
enough to guess limits precisely. For instance, as we will see later,
2n and 5n have the same order, namely n, but when we
form fractions from them by dividing them by n, the resulting ratios
have different limits at infinity (2 vs. 5).
Therefore we introduce another comparison. It does not have a formal name, in
fact it is not really covered precisely in calculus texts, therefore we will
just use the phrase that two sequences "behave the same at infinity", and use
the notation ∼.
Definition.
Consider sequences {an} and
{bn}.
We say that an has higher order
(at infinity) than bn, denoted
bn = o(an),
if

We say that the two sequences are of the same order (at infinity) if there
is a positive real number A such that
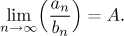
We say that the two sequences behave the same at infinity,
denoted an ∼ bn,
if
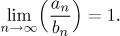
Note that
bn = o(an)
can be also equivalently defined by
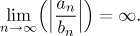
(We had to put the absolute value there, since 1/0 need not have a limit or
it can go to plus/minus infinity, while
1/|0| = ∞.)
What is the use of the these notions? Order allows us to get a feeling for
speed of growth, it focuses on the substance and ignores the less important
factors. For instance, it is easy to check by definition that
n2 is of higher order than n. It is equally easy to
check that n is of the same order as 135n. Why should it be so,
when we know, that 135n goes to infinity faster than n?
The reason is simple. We know from experience that n2 gives
much larger answers than n when large numbers are substituted in. Now
consider a really large multiple of n, for instance
1000000n.
If we substitute smaller numbers for n, then 1000000n will be
larger than n2. However, as we put in larger and larger
numbers, sooner or later the formula n2 will win over
1000000n, by which we mean that it will give much larger answers,
larger by as much as we want. From the point of view of n2
there is therefore little difference between 1000000n and n, it
beats both with equal ease. To be more precise, when we divide
n2 by 1000000n, or by n, the resulting ratio
goes to infinity, which means that n2 is substantially
larger than the other two; on the other hand the ratio
1000000n/n does not go to infinity, so
1000000n is not
substantially larger than n.
This is true for any expression A⋅n and suggests that
these expressions should be put into one category, for which n is the
natural representative.
Order thus sorts expressions into groups, within groups there might be some
comparison (surely 2n grows to infinity faster than just n),
but the difference is not large; the important thing is than any member of
one group beats any member of another group if that group is of lower order.
We typically take the simplest possible representant for each group, or each
"type" as we commonly say, for instance expressions like
2n,
−3n, (n − 5),
(n2 + 13)/n
are all of the type (order) n.
The most popular types are represented by powers, exponentials, powers of
logarithms, factorials and general powers. Direct application of order allows
us to tell readily the limit of a ratio of these types, assuming that we can
establish some general order comparison.
However, the biggest benefit comes from combining order and the "behave the
same" relationship. While order is too rough to guess the limit precisely,
when two sequences behave the same, the have the same limit at infinity. This
allows us to replace more complicated expressions with simpler ones that
behave the same, which makes subsequent work much easier. The most natural
way of creating those simpler expression is to use the order: all parts of an
expression that are of lower order can be often ignored. We talked about it
in the section Intuitive
evaluation in Theory - Limits. Now it is time to make this precise.
Fact.
If an→L
and
an ∼ bn,
then
bn→L.
This shows the main benefit of comparison. Now we will state precisely how we
can simplify sequences.
Fact.
If
bn = o(an),
then
(an + bn) ∼ an.
In words, when investigating the limit of a sum, we can ignore the added
parts of lower order without making a mistake. The proof of this fact is
actually very simple. We have to prove that the ratio
(an + bn)/an
converges to 1. We can divide the fraction and get
(1 + bn/an).
Since it is assumed that an is of higher order than
bn, the ratio in parentheses converges to zero and
consequently the whole fraction converges to 1, exactly as needed.
Now if these two facts, along with the
scale of powers, get
properly proved, the intuitive evaluation we talked about actually becomes a
proper and correct mathematical method, no further proofs are needed to
confirm its findings! Unfortunately, as we remarked, this theory is not
covered by (pretty much all) calculus textbooks and courses, so we will not
rely on it in Math Tutor either; we will just use it as a supplemetary method
and confirm the guessed answers by more common methods (like the factoring
out trick). This does not mean you cannot try it at school, but before you
start handing in tests with results justified by mere "exponentials beat
logarithms", make sure you understand the topic well; the examiner is sure to
have some questions concerning your justification and if you cannot answer
them...
As we mentioned above, powers and similar expressions are the most popular
types people compare, although there are many more types; however, these are
less usual. In Intuitive
evaluation in Theory - Limits we established a scale of powers; we
actually claimed the following things:
n! = o(nn),
an = o(n!) for
all a with |a| > 1,
nb = o(an)
for all
|a| > 1, b > 0,
[ln(n)]c = o(nb)
for all b > 0,
c > 0.
All these can be proved, some by l'Hospital's rule, others by comparison (see
Appendix below). We also claimed that within each cathegory, the expression
with larger constant is of higher order:
If
|a| > |b| > 1, then
bn = o(an),
If
a > b > 0, then
nb = o(na),
If
a > b > 0, then
[ln(n)]b = o([ln(n)]a).
Here the proofs are very simple, when you form the apropriate ratio to
confirm some claim, you will see that you can cancel.
One interesting fact about the order is that it yields nice
relations. Namely, the relation of being of the same order is an equivalence
and the relation of being of higher order is transitive. This in
particular means that once we establish the above facts about powers,
exponentials etc., we can automatically also use other comparisons that go
via some middle man; for instance, we then automatically have that
ln(n) = o(n!).
In fact, we could do the same considerations as above for two functions,
f (x) and g(x),
defined on some
(K,∞),
and wonder how they
compare when x gets large. Everything would be the same, after all, as
we remarked in the beginning, the notion of order is very general. We look at
it closer when investigating functions, see
order of functions
in Functions - Theory - Limits.
Appendix: The scale of powers proved
Claim
n! = o(nn):
This is best done by one-sided
comparison and smart grouping of the ratio.

Claim
an = o(n!)
for
a > 1: This is proved similarly as the previous case. By
[a] we denote the integer part of a, that is, the largest
integer that is less than or equal to a.
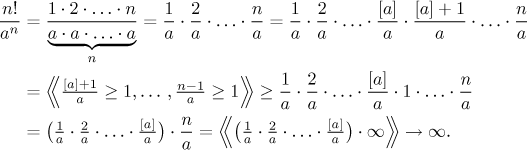
Claim
nb = o(an)
for a > 1: This is done by passing to functions and the
l'Hospital rule. We start with
the case b = 1:
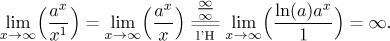
If b is a positive integer, the proof is done by repeating the
l'Hospital rule b-times. Formally, it is best done by induction, we
already did it for b = 1 and now we prove it for b,
assuming that we already established it for
b − 1:

If b > 0 is not an integer, consider some integer
c that is larger than b. Then
(c − b) > 0, hence
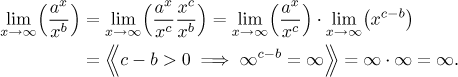
Claim
[ln(n)]c = o(nb):
This is also done by the l'Hospital rule. Procedure is similar to the previous case,
the proof is done in three steps, one of them by induction. We will therefore
not repeat the procedure, we will just show how the proof goes if we try to
show directly the case c = 2; then the l'Hospital must be used twice.
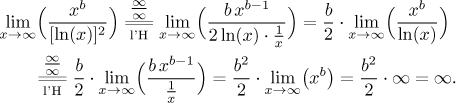
![]()
![]()
![]()