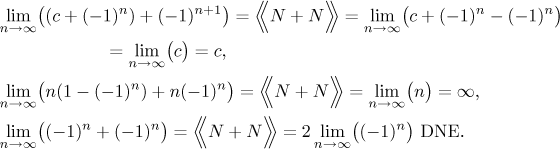
Here we list algebra of expressions that do not have a limit (not even infinity or minus infinity). We will use the symbol N for a sequence without a limit. In a Note at the end we will also briefly discuss some indeterminate expressions involving N.
Since sequences whose limits do not exist are not encountered very often, there is usually little attention paid to this kind of algebra; in fact, the following list is probably the only one that you will find anywhere. This shows that this topic is not all that important, which is a good excuse for not listing all possible combinations; after all, sequences without limit can have all kinds of troubles in them and a complete list would be very long (especially if we wanted to treat indeterminate expressions properly).
Addition/subtraction:
Indeterminate expressions:
Multiplication/division:
Indeterminate expressions:
Powers:
Indeterminate expressions: for instance
We will show some examples to convince you that we correctly listed some
expressions as indeterminate. For N we will use
The expression
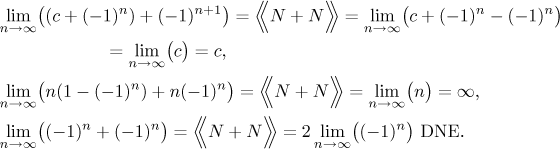
The expression
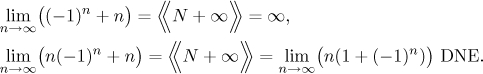
The expression
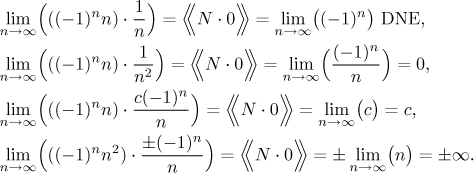
The expression

The expression
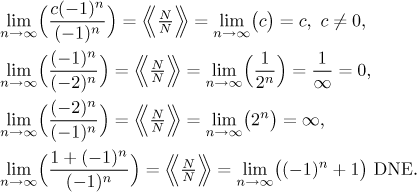
The expression
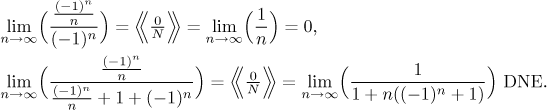
The expression
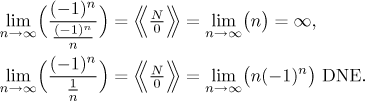
The expression
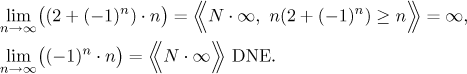
The expression

The expression
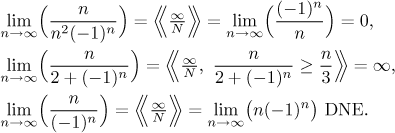
The expression
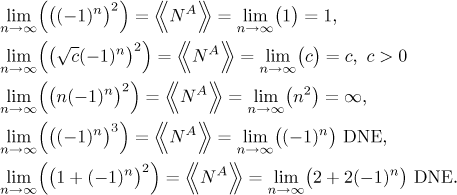
The expression

The expression
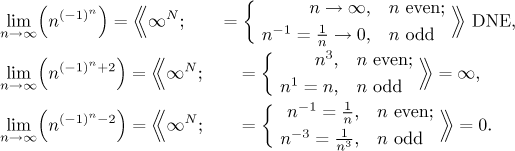
The expression
