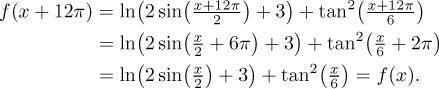Periodicity of a real function: Survey of methods
There is no algorithm for finding periodicity, we usually guess and then
confirm or rule out our guess. Thus we have two topics here. First, how we
confirm/rule out a certain period, and second, how do we make a guess.
Confirming periodicity. Assume that we have a function f and we
suspect that a certain T > 0 is a period. This assumption is best
checked by the definition, that is, we have to show that for any x,
f (x + T ) = f (x).
If this works, our
assumption was correct. If this equality fails for even one x, then
this T is not a period.
Here we will prove that the tangent is actually
π-periodic, using some trig
identities.
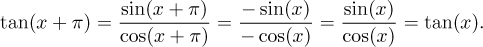
Guessing periods. This is based on two ingredients. First, we do know
that some functions are periodic with certain basic periods. In fact, most
people know only four such functions, namely sine and cosine with basic the
period 2π,
and tangent and cotangent with the basic period
π.
Second, we need to know what happens to a certain period if we start
combining functions together. These facts can come handy:
• If f is T-periodic, then
f (Ax + B) is
(T/|A|)-periodic
(note that the value of B is irrelevant, that is, shift in
argument does not influence periodicity). On the other hand,
Af (x) + B is again
T-periodic, that is,
transformations of the value of f do not influence periodicity.
• If f is T-periodic, then
| f | is also
T-periodic. Note that the basic period may change now, for instance
sin(x) is
2π-periodic, while
|sin(x)| is
π-periodic.
On the other hand, f (|x|) need not be periodic at all, for
instance tan(|x|) is not periodic.
• If g is T-periodic, then the composition
f (g)
is T-periodic for any function f. Again, note that the basic
period may change, after all,
|sin(x)| is a composition of the
2π-periodic sine and
non-periodic |x|. On the other hand, having the outer function
f periodic does not guarantee anything about the composition.
• If f is T-periodic and g is
S-periodic, then
the functions f + g,
f − g,
f⋅g,
and
f /g are R-periodic, where R is the least
common multiple of S and T. Again the basic period may change,
for instance tan = sin/cos and the basic period is halved. By the way, the
least common multiple is usually done for integers, but T and S
need not be integers, so to be precise we add an exact statement:
R is the smallest positive number such that
R/T and
R/S are integers.
Example: Determine the periodicity of
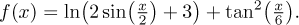
Solution: We have a sum of two functions, so we start by investigating
each term separately.
Inside the first term we have sine with scaled argument, so by one rule
above, sin(x/2) has period
2⋅2π = 4π.
This function is then scaled twice and shifted up by 3, which does not
influence the period. Then we apply the logarithm to it as the outer function
in composition, so the outcome is again
4π-periodic.
By the way,
this is still the basic period, the logarithm does not influence it, but this
is not really important now.
In the second term inside we have a tangent of a scaled argument, so the
original period
π will be multiplied by 6
according to one rule above. Thus tan(x/6) is
6π-periodic.
This functions is then squared, and as we observed, this does not influence the period.
So we are adding two terms, one
4π-periodic, the other
6π-periodic.
The rule above says that the sum should have the least common multiple as
period, so we would guess that the given function is
12π-periodic.
Now we need to check that this is correct:
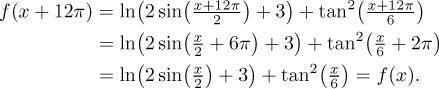
The proof is complete, our guess was correct. In fact, this is also the basic
period, but proving such a thing is not all that easy in general, so we will
leave this topic.
For more examples see
Solved Problems.
Continuity
Back to Methods Survey - Basic
properties of real functions
![]()
![]()