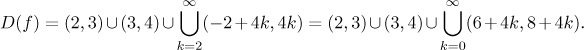Problem: Determine the domain of the following function:

Solution: There is a general power (the root), so we have to start by rewriting it using the "e to ln" trick:

Now we are ready to look for trouble:

1. The outside logarithm requires that its argument be positive: log₃(log₂(x)) > 0.

2. The middle logarithm requires that its argument be positive: log₂(x) > 0.

3. The inside logarithm requires that its argument be positive: x > 0.

4. Passing to the exponential, its argument can be arbitrary, so we look at the argument by itself. First we see the little fraction, its denominator cannot be zero: x² ≠ 0, that is, x ≠ 0.

5. Then we have the logarithm, its argument should be positive:

6. Cosine eats anything, so we move on. The next term is 2^x, which accepts any real number. So we go to the last term, it's a fraction so we need a non-zero denominator.

7. The logarithm requires

that is, x > 1.

Now we look closer at the conditions that require further work.

Condition 1: If we raise both sides of the inequality as arguments of 3^x and cancel "3^log₃", we get log₂(x) > 3⁰ = 1.

Now we raise both sides as the argument of 2^x and we get x > 2¹ = 2.

Condition 2: If we raise both sides of the inequality as arguments of 2^x and cancel "2^log₂", we get x > 2⁰ = 1.

Note that the conditions 1, 2, and 3 are of similar type and gradually less and less restrictive, so later during the intersection phase we can disregard the 2nd and 3rd and only consider the first, x > 2.

Condition 5: This is best done by first considering cos(y) and asking when is this positive. By looking at the graph of cosine we see that y must belong to or some shift of this interval by 2π. In the language of inequalities:

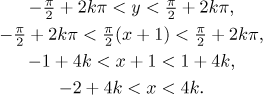
Thus x must belong to the interval (−2,0) or some shift by 4, that is,

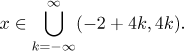
Condition 6: By taking the exponential of both sides and cancelling "e^ln" we get the condition (x − 1)/2 ≠ e⁰ = 1, that is, x ≠ 3.

Now we make an intersection of all conditions

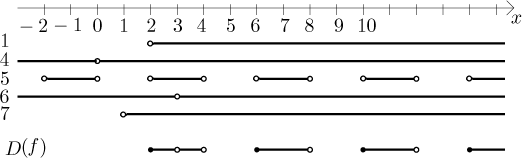
and get the answer:

Next problem
Back to Solved Problems - Real functions