Problem: Determine the constants a,b for which the
following function is continuous.

Solution: Since both ax and the expression in the
third alternative are continuous functions on their domais, it follows that
the given function f is also continuous on open sets where it is given
by these expressions. Thus we have continuity at all points apart from 2. We
see that this question is really about continuity at 2. What is needed there?
We need both one-sided limits to exist, converge and be equal to
f (2) = 8.
We start with the limit from the left, to the left from 2 the function is
given by ax.
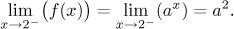
For continuity we need f (2-) = 8, that is,
a2 = 8. This equation has two solutions, plus and
minus root of 8, but since a is supposed to be the base of an
exponential, it cannot be negative. Thus we set a to be the positive
root of 8 to get continuity from the left.
Now we address continuity from the right, to the right from 2 the function is
given by the fraction.
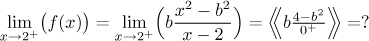
If we want to have any chance of convergence, we need to neutralize the zero
in the denominator. One possibility is to put
b = 0, but
then the whole expression is identically zero and therefore also
f (2+) = 0, so there si no chance of making this
into 8. Therefore 0 is not the right choice for b. The other
possibility is to make the numerator zero in the limit, which means that
b2 should be 4. There are two possibilities, b can
be −2 or 2, and we check whether any of them makes the limit equal to 8. Note
that these two values of b are the only hopes for making the function
continuous at 2 and if none of them work out, then the function simply cannot
be made continuous at 2.
First we try b = −2.
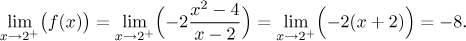
This is no good. We try b = 2.
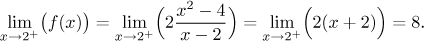
We got lucky, this is the right value for b.
Conclusion: The function f is continuous for the values

Next problem
Back to Solved Problems - Real
functions


![]()
![]()
![]()
![]()
![]()