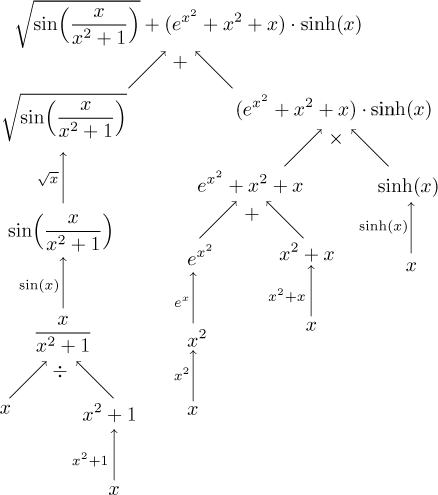
When we work with a function defined by some formula, an important role is played by the order in which the formula is evaluated when a number is substituted in. A typical function is formed by combining elementary functions using the four basic operations (addition/subtraction, multiplication and division) and composition. No matter how a complicated such a function gets, we can always capture its structure using a tree. Before we get there, we look at some examples.
Example:
Consider the function
Since polynomials are considered elementary functions, we can think of
evaluating the expression
Translated into mathematics, we see that we start by applying the function
![]()
However, in most applications we want to see it from the other end, in the order "last to first". The best way to draw it is to put x down as a root and let the function grow up from it.
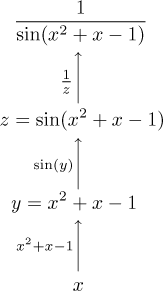
We used variables y and z to emphasize the composition
procedure, but in more complicated functions this is not feasible. We will
therefore keep using the variable x in individual functions, for
instance in this example we would say that we applied
This seems trivial, we just turned the picture. What is the point of all this? The next example will show some.
Example: Consider the function
![]()
Now we start evaluating. Take some concrete x, put it into your
calculator and apply
It is better to start from the "outside", with the operation that is done last when evaluating the expression, which is the logarithm, and then look at what is done before that, the division, which naturally shows two branches going down.
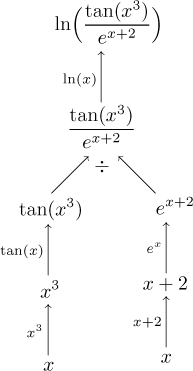
If this all seems simple to you, that's great, it means you should not have any trouble in calculations where the order comes into consideration. Just to be sure, try to decompose and draw a tree for this function (do it on your own, don't peek below):
![]()
If you got the same tree as we did, you will be fine.