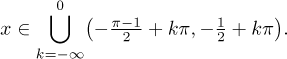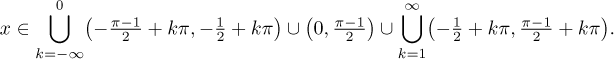We will here solve the inequality by dividing by x, and we have to
distinguish two cases:
a) x > 0. Then we just divide and we
get sin(2x + 1) > 0. This
can be solved for instance by imagining the graph of
sin(y).

We see that sin(y) is positive exactly if y is from the
interval (0,π) and its
shifts by 2kπ for
k any integer. For our case this means that the expression
2x + 1
must belong to one of the intervals
(2kπ,π + 2kπ).
We can write it as an inequality (or rather, two inequalities)
2kπ < 2x + 1 < π + 2kπ,
solving it for x (we can solve both simultaneously) we get
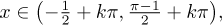
where k can be any integer.
However, now we have to recall that we were doing this solution only under
the assumption that x > 0, so we can only take the part of this
solution that includes positive numbers. If
k > 1; the corresponding
intervals lie on the positive x-axis and so they survive. For
k < 0, the corresponding intervals only include negative numbers and
so they can be ignored. If k = 0, we get the interval
(−1/2,π/2 − 1/2)
whose part lies in positive numbers, so we take only that part. Thus we get
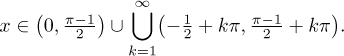
b) x < 0. Now when we divide we have to switch the direction of the
inequality, thus we get
sin(2x + 1) < 0. As before, from the graph of
the sine function we conclude that now 2x + 1 must belong to one of the
intervals
(−π + 2kπ,2kπ).
We can think of it as of inequality
-π + 2kπ < 2x + 1 < 2kπ,
solving it we get
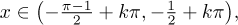
where k can be any integer.
As before, we have to recall now that we were doing this solution only under
the assumption that x < 0, so we can only take the part of this
solution that includes negative numbers. Thus we get
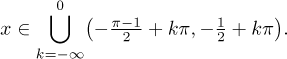
c) To cover all possibilities, we should actually also check what happens when
x = 0, and we immediately see that this is not a solution of
the given inequality, so this case does not add to our solution.
Since we had a choice
of three variants here, we get the final solution by taking a union of the
partial solutions:
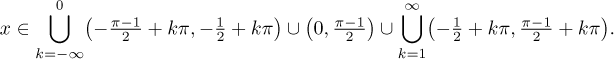


![]()
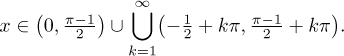
![]()