Angles

The most popular unit for measuring angles is the degree. There is 360 degrees to a full circle, 90 degrees is the right angle. There are essentially two ways of specifying the angle between two rays.

1. If the rays are of the same importance, we get an angle that is not oriented (for instance between the sides of a triangle). Given two rays, we always take the smaller angle, measure it and express the answer as a positive number (or zero).

2. If one ray is in some way special (for instance the x-axis in a coordinate system), we usually use an oriented angle, taken positive in the counterclockwise direction (towards the y-axis) and negative in the clockwise direction.

We see that now the same angle can be specified in several ways. In fact, it can be specified in infinitely many ways, since in this situation we can go around the origin several times, each time gaining a full circle (360 degrees), and we can do it both ways.

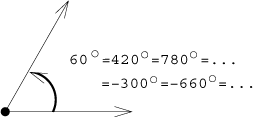
Degrees are "practical". People use them when working with geometrical objects, calculating distances and angles "in the real world" and situations like this. Since they correspond to directions on a compass, we are pretty familiar with them. In such settings we also often use the non-oriented angle.

However, in sciences, most notably in math and physics, we (almost) always use the oriented angle and prefer a different unit for it: the radian.

Radians

Given an angle, we obtain its size in radians by dividing the arc length by the radius.

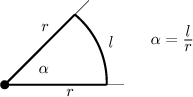
This is one great advantage of the radian, since in situations as in the picture we calculate the arc length as (angle)⋅(radius). This is very useful in theoretical calculations.

The full angle is (circumference)/(radius), that is, the full angle is 2π. Similarly we easily calculate (or guess) the important four angles:

The relationship between degrees and radians is linear, so we have simple transformation formulas:

Probably the most popular angles are these:

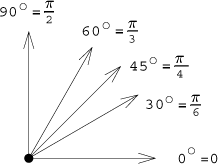
Why are they popular? π/2 is the right angle, its importance is hopefully clear. The angles π/4 and π/6 represent the half and the third of the right angle, they appear quite often. Finally, π/3 is exactly the angle that appears in an equilateral triangle.

Note that if we make a right-angle triangle with another angle π/3, then the third angle must be π/6. Also, an isosceles right-angle triangle has the two other angles equal to π/4. So it would seem that these angles appear in geometry rather often.

By adding/subtracting right angles we get the whole "compass rose":

Trig functions and degrees/radians

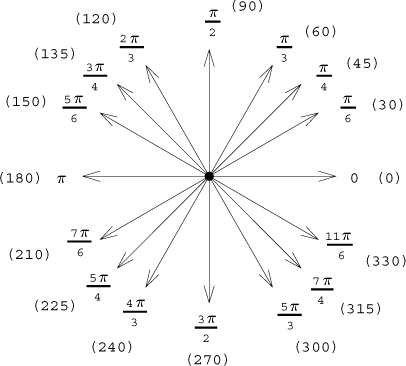
Since the two units are tied linearly, one can use any of them for measurement with no trouble. However, things change when we start using these measurements in calculations. In particular, we have to be careful how we substitute angles into trig functions. The tables of, say, sine are different for angles measured in degrees and for angles measured in radians. For instance, if we have sine that expects radians, we get sin(π/2) = 1. But if we put 90 into it, this sine will think that we mean 90 radians, which is something like going 14 times around the origin (2π can be put 14 times into 90) and we still have some 2.035 radians left, thus we would get

sin(90) = sin(2.035rad) = 0.8939.

For 90 degrees we need a different sine, the one that expects degrees. This is actually a popular source of errors in calculations, when a student forgets to switch his calculator into degrees (or radians, whichever is needed).

Thus "sine in degrees" and "sine in radians" are two entirely different functions. In mathematics, physics and other sciences we need a precise specification, so long time ago it was decided to stick with radians. As we remarked, radians are better for scientific calculations, so this makes perfect sense, and it actually gives much nicer formulas. For instance, for derivative we have [sin(x)] ′ = cos(x). If we take a derivative of the "sine in degrees", we get a different (and not so nice) formula!

In conclusion, remember that in calculus all trigonometric function only eat radians.