Theorem (limit and continuity).
Let f be a function defined on a neighborhood of some
real number a. If f is continuous at a,
then
![]()
We start by looking at a few basic properties of limits. Then we look at theorems used in evaluating limits. This leads directly to the limit algebra, our main tool for evaluating limits. Another topic it leads to is one-sided results of limits, an important ingredient. At the end of this section we will look at connections between the limit and some properties: boundedness, monotonicity, sequences etc.
The following statements should be clear if you understand what limit means. In all these statements, a can be a real number or (negative) infinity.
Fact.
Let f be defined on some reduced neighborhood of a. Then f converges to L at a if and only if( f − L) converges to 0 at a.Fact.
Let f be defined on some reduced neighborhood of a. If f goes to L at a, then| f | goes to|L| at a.Fact.
Let f be defined on some reduced neighborhood of a. Then f goes to 0 at a if and only if| f | goes to 0 at a.Fact.
Let f and g be defined on some reduced neighborhood of a. Assume that both converge at a. Their limit at a is the same if and only iff − g goes to 0 at a.
Note that the last statement is not true any more if we drop the assumption about convegence. As usual, all these statements are also true for one-sided limits. This is also true for the following theorem:
Fact.
If f has a non-zero limit at a, then there exists a reduced neighborhood U of a and a constantk > 0 such that| f | > k on U.
For details see separation from 0 in Continuity in Functions - Theory - Real functions.
When we evaluate limits, we always have to start from something that we know. The first source of such limits is this theorem, in fact just a reformulation of a theorem we had before.
Theorem (limit and continuity).
Let f be a function defined on a neighborhood of some real number a. If f is continuous at a, then
The same is true for one-sided limit and one-sided continuity, there we just need existence of f on a one-sided neighborhood. This theorem is quite useful, since we know that all elementary functions are continuous on their domains and so are functions obtained from elementary functions using algebraic operations.
Example: The limit of
Example: We look at the limit at 2 of
![]()
The theorem as such does not help here, since g is not given by some
obviously continuous function on any neighborhood of 2. However, it is given
by x2 on some left neighborhood of 2, therefore we can find
the limit of g at 2 from the left by substituting
g(2-) = 22 = 4.
What about the limit from the right? The function g is not given by
any obvious continuous function on a right neighborhood of 2, so this won't
be so easy. Only at the first sight, though. Note that the function
g(2+) = 4.
Since the limit of g at 2 from the left and the limit from the right exist and agree, it follows that g has a limit at 2 equal to 4.
We see that the theorem can be also applied in more general situations, we can obtain a limit of a function f at a by substituting into some expression assuming that this expression by itself is a continuous function at a and is equal to f on some reduced neighborhood of a. An analogous statement is true for one-sided limits.
We know that any expression we create using elementary functions and algebraic operations plus composition is continuous on its domain, and we can recognize whether a lies in this domain simply by trying to substitute a into this expression. From this we get the following rule.
Basic rule for evaluating limits at proper points.
Assume that a function f is defined by some expression on some reduced neighborhood of a real number a. If we substitute a into this expression and it makes sense, then the outcome is the limit of f at a.
Appropriate rules are true also for one-sided limits. There f needs to be defined by a suitable expression on some one-sided reduced neighborhood of a.
Note one trivial case: When we substitute any a into a constant, we get this constant. We also saw in the example above how we can use this rule even if a function is not given by one formula, but by different formulas on each side of a. We then pass to one-sided limits and compare outcomes. This comes handy especially when we work with split functions.
This rule is very useful; however, it would be too easy. In most examples something goes wrong. What can go wrong? If f is not defined by some nice formula on a (one-sided) reduced neighborhood of a, then (unless f is some weird function) the function is not defined on a reduced neighborhood of a and the limit does not make sense. Thus the only interesting case is when f is defined by some expression on a reduced neighborhood of a, but a itself causes trouble when we substitute it into this expression. In other words, a is exactly at the boundary of the domain of this expression.
This situation can be also extended to cases when a is improper, we can consider an expression that is defined on a neighborhood of infinity and we ask for a limit at infinity, similarly for negative infinity. What can we do then?
Some cases are simple. For all elementary functions we know what happens at
the endpoints of the intervals of their domains. For instance, we know that
the limit of
It gets more interesting when we start putting such functions together. We need to know how to put information about limits of simple terms together.
Theorem (limit and algebraic operations).
Let a be a real number, ∞, or−∞. Let f,g be functions defined on some reduced neighborhood of a. Assume that f has limit A at a and g has limit B at a. Then the following is true:
(i) For any real number c, the function(c⋅f ) has limitc⋅A at a if it makes sense.
(ii) The function( f + g) has limitA + B at a if it makes sense.
(iii) The function( f − g) has limitA − B at a if it makes sense.
(iv) The function( f⋅g) has limitA⋅B at a if it makes sense.
(v) The function( f /g) has limitA/B at a if it makes sense.
(vi) The functionf g has limitAB at a if it makes sense.
Now what is that remark about making sense? If A and B are real
numbers, that is, if the two given limits are convergent, then the operations
(i) through (iv) always make sense. However, the ratio
We could present a theorem now with many statements, but it is much easier to start from another end. Note that in the theorem above we did not assume that A,B are finite, and some operations can be defined also for cases when they feature infinity. If we use these operation in the above theorem and deem that they "make sense", then all the results we obtain in this way are correct. What operations can we introduce?
If for instance (close to a) f is immensely huge
and g is about 1, then
What do we get if we add or multiply two immensely huge
numbers? Another immensely huge number. We just argued that
On the other hand, we do not know what
This shows that the "making sense" for
working with limits is different from making sense for numbers.
The reason is that now the numbers A,B do not represent real
numbers, that is, fixed quantities, but outcomes of limits, in other words,
they represent processes, "almost numbers". This has the effect that some
operations, although they can be performed with real numbers, do not work
with limits. The best example is the power
After all, in "normal" algebra we have
To summarize, the algebra of limits allows us to calculate more complicated limits using the basic limits, we just need to remember what works, what surely does not work, and then there are indeterminate expressions that must be handled individually. You will find more details in the note on limit algebra, we also offer a brief list.
We still did not cover one important operation, that of composition.
Theorem (limit and composition).
Let a be a real number, ∞, or−∞. Let f be a function defined on some reduced neighborhood of a, assume that f has limit A at a. Let g be a function defined on some reduced neighborhood of A, assume that g has limit B at A. If at least one of the following two conditions is satisfied:
1. g is continuous at A, or
2. there is a reduced neighborhood of a on whichf ≠ A,
then the limit ofg( f ) at a is B.
This theorem is a bit technical, but for practical considerations we may
simply remember that if f goes to A at a and g is
continuous (which most functions that we meet are), we get the limit of
Example: We know that
This in fact nicely fits with the "substitute and see" concept. The two theorems on limits and the limit algebra with infinities allow us to extend the basic rule for evaluating limits to all cases:
If we want to find a limit at a (which now can be also improper) of some expression defined on a reduced neighborhood of a, then we "substitute" a into this expression and if the answer (obtained using the limit algebra) makes sense (it might also be improper), then the outcome is the answer to the limit.
We put "substitute" into quotation marks, since infinity is not really a number, so it would not be proper to call what we do substituting. Likewise, the limit algebra is not a "real" algebra. Although it is possible to do the limit algebra properly with definitions and theorems and all, most profs do not bother, which makes the limit algebra kind of illegal, some profs are even allergic to when you start treating infinity as a common number. To be on the safe side, do calculations with infinity on the side; here in our calculations we put them, along with other remarks, between big double angled braces ⟪ and ⟫ to indicate that they are not parts of the "official" solution.
One last remark concerning this substituting business. When the expression involves a general power, we should always rewrite it into the "e to ln" form.
We can rewrite both theorems in another way. They can be used to delay some parts of the limit for later, to split the limit into parts so that we can apply different methods to each part etc. The basic idea is that we can "pull things out of the limit" so that what is left in it becomes simpler. The first theorem allows us to perform algebraic operations outside of limits, assuming that what we get at the end makes sense. The second theorem allows us to pull out nice (continuous) outer functions out of limits, again assuming that what we get in the end makes sense.
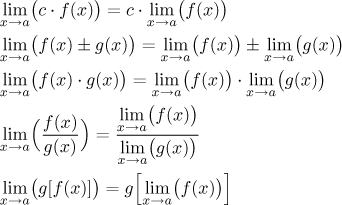
Example: We will put all details into it to show how we think. An experienced student would write just the first and the last line.
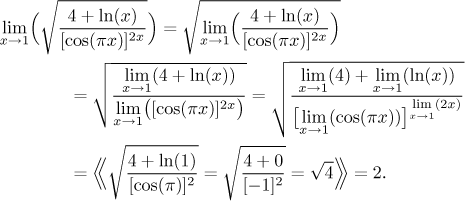
We could actually find this limit using the "substitute and see" method, but we wanted to show the use of these rules on something simple.
Note that the equalities in the rules above are "conditional". When you split a limit into several smaller ones, you do not know whether this equality is correct. Only after you finish calculating all the smaller limits, put the outcomes together using limit algebra and it makes sense, then you can say that the equality was correct and the final outcome is a valid answer to the original limit.
On the other hand, if you finish all individual limits and it turns out that
you cannot put these answers together using the limit algebra, then the
conditional equality is wrong, the original limit might be anything. A simple
example: The constant function 1 has limit 1 at infinity. However, if we
write it as
A small modification of this example shows a very important rule: Unless you know what you are doing, always finish all parts. In particular, if you split a limit of a product into a product of smaller limits and one of them comes up as zero, you cannot stop calculations and claim that the whole thing is zero. Granted, zero times a number is again zero, but that only works in the usual algebra. In the limit algebra we can also have "zero times infinity", which is an indeterminate product that can be anything. Returning to that simple example, we can try the limit at infinity like this:
Obviously it would be a mistake to stop once we saw that the first limit was zero, but after completing the other part we see the indeterminate product and know that it was not a good idea to split the original limit into two. For more details, see this note.
When using these rules and approaches, one might encounter several problems. One possible problem is that you use the limit algebra and end up with an indeterminate expression. Then one has to use various tricks to (try to) figure out the outcome. Some tricks come in the following sections, a practical review of useful methods can be found in Methods Survey.
Another problem we sometimes stumble upon concerns one-sided limits. Namely,
when substituting into some functions, we can only go from one side, which
should be somehow reflected in this limit algebra. For instance, we cannot
write
Example: We will look at the limits of
Similarly, we often run into trouble with the expression
In a simple straightforward situation with a one-sided limit we simply use
the above rules, but what if we have a function that goes to zero in the
denominator? For instance,
This problem is fixed by considering one-sided results to limits. We will cover this in the next part.
If we want to use the limit algebra in a situation when we compose functions and the outer function requires a one-sided argument, we can only work out the answer if we know some information about the outcome of the limit of the inside function. This suggests that we look closer at how a limit value is approached. Compare these three graphs:
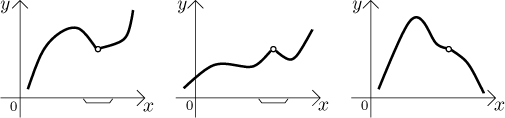
In all three cases the limit at
Definition.
Let a be a real number, ∞, or−∞. Let f be a function defined on some reduced neighborhood of a, assume that f has a proper limit L at a.
We denote this limit L+ if there is some reduced neighborhood of a such thatf > L on that neighborhood.
We denote this limit L- if there is some reduced neighborhood of a such thatf < L on that neighborhood.
Similarly we define L+ and L- for outcomes of one-sided limits.
In most cases such distinction is irrelevant, we simply say the limit is 1 and it works, but in some cases this can be very important.
We return to the example above, when we looked at limit at 0 of the
functions
When x approaches 0, then the function x2 goes to 0
and also
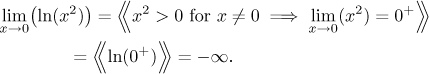
On the other hand, even when x is very close to 0, then
x3 can be both positive and negative, therefore its limit
at 0 cannot be written as 0+ or 0-. Consequently we
cannot put it into logarithm, a clear indication that there is something
fishy about
Similarly we now easily determine the limit of
However,
Example: Compare the following two problems:
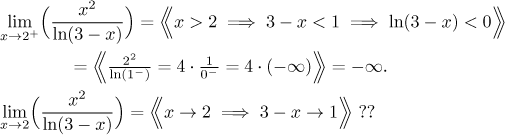
In the first problem we argue like this. When x goes to 2 from the
right, it means that x is something like 2 plus a little bit, say
On the other hand, if x goes to 2 from both sides and gets close, then the logarithm comes up almost zero, but sometimes positive and sometimes negative, depending on which side of 2 x is. Since we are unable to specify the 0 in the denominator, we cannot make any conclusion. In fact, since we cannot force the 0 to be plus or minus, we suspect that the limit in question does not exist. To check we try to look at the limit at 2 from the left:
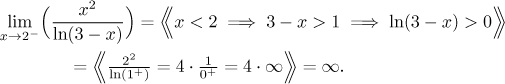
Since the limit at 2 from the right is different than the limit at 2 from the left, the conclusion is that the limit at 2 does not exist.
Remark: Although very often one-sided results appear when calculating
one-sided limits, these two are not really related. One can get a one-sided
result when calculating a both-sided limit, we saw such situation when
looking at the limit of x2 at 0. On the other hand, it can
also happen that one has a one-sided limit, but the answer is not one-sided.
For example, the limit of x⋅sin(1/x) as
x goes to 0 from the right is 0, but thanks to the wild and never
ending oscillation, the function never settles down to a positive or negative
part, hence the result of this limit cannot be 0+ or
0-. For more info about this function (for instance its graph) see
Theorem.
If a function converges at some a, then it must be bounded on some reduced neighborhood of a.
This definitely does not go the other way around, the example of
Now we will look at monotonicity. The existence of a limit (or convergence) does not imply anything about monotonicity, which seems clear, we know that a function can go to its limit in crazy ways. However, we do get some information out of monotonicity.
Fact.
A function that is monotone on some reduced left neighborhood of a point a has a limit at a from the left.
A function that is monotone on some reduced right neighborhood of a point a has a limit at a from the right.
Here a may be also improper. We get more if we put together boundedness and monotonicity.
Fact.
A function that is monotone and bounded on some reduced left neighborhood of a point a has a convergent limit at a from the left.
A function that is monotone and bounded on some reduced right neighborhood of a point a has a convergent limit at a from the right.Corollary.
A function that is monotone on an interval has convergent one-sided limits at all its inner points and also the appropriate one-sided limits at endpoints must exist.
Again, this includes the case of improper endpoints.
We start with a nice theorem.
Theorem (Heine).
Let a be a real number, ∞, or−∞. Assume that a function f has a limit L at a. Then for every sequence{an} such thatan→a andan ≠ a we havef (an)→L.
We used this theorem when working with sequences. This theorem also works in the opposite direction, but it is not really good for finding limits of functions, since we would have to try all possible sequences that go to a, substitute them into f and see what they do before we could say anything about the limit of f.
However, as stated this can be useful in showing that some limit does not exist.
Example: We will show that
Consider two sequences,
Now if the sine had a limit at infinity, then by the above theorem, both
You can learn more about the interplay between functions and sequences in section Sequences and functions in Sequences - Theory - Limits.