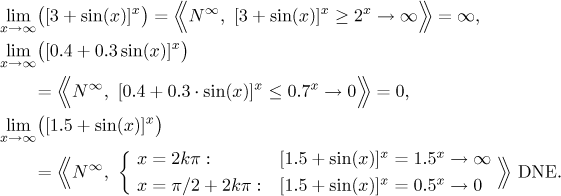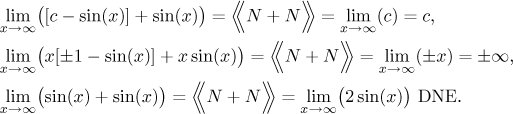
Here we list (a part of) algebra of expressions that do not have a limit (not even infinity or minus infinity). We will use the symbol N for a limit that does not exist. In a Note at the end we will also briefly discuss some indeterminate expressions involving N. Some examples there are quite involved and interesting, so we look at them in Solved Problems.
Since this kind of considerations is done rarely, the necessary properties are usually worked out on the spot. We made a list here since we were curious and also for the sake of completeness, but since everybody seems to live happily without it, we took it as a good excuse for not listing all possible combinations (there is too many of them).
Addition/subtraction:
Indeterminate expressions:
Multiplication/division:
Indeterminate expressions:
Powers:
Indeterminate expressions: for instance
We will show some examples to convince you that we correctly listed those indeterminate expressions.
The expression N + N:
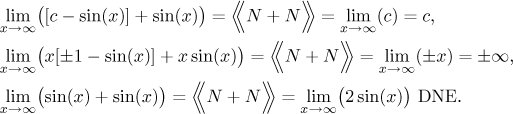
The expression N±∞:
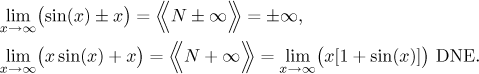
The expression 0⋅N:

The expression N⋅N:

The expression 1/N:

The expression N/N:
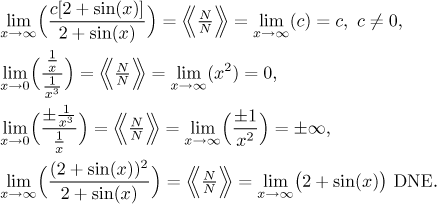
The expression 0/N:
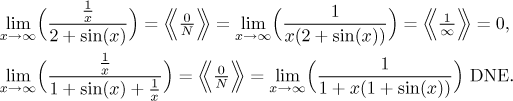
The expression N/0:
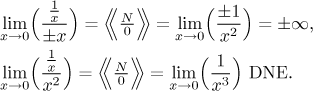
The expression N⋅∞:
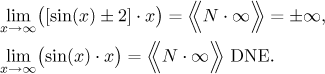
The expression N/∞:
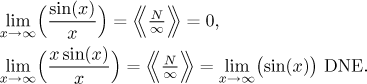
The expression ∞/N:
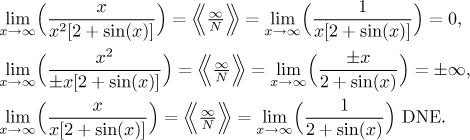
The expression NA:

The expression 1N:
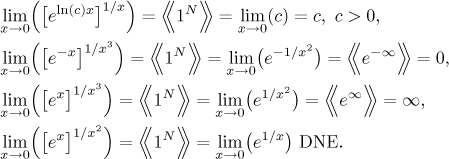
The expression ∞N:
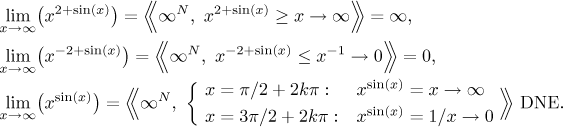
The expression N∞: