Problem: Identify the shape of the parametric curve
x = e^t − 1,
y = e^2t − 2e^t for t real.

Solution: There is no point in using some theorem, because it would only (with a bit of luck) guarantee a local existence, while we want a global and concrete description. We could also try the standard procedure for drawing parametric curves (see Parametric functions in Derivative - Theory - Graphing, or Parametric functions in Derivative - Methods Survey - Graphing), but that would only give us a sketch, while the question says "identify". The only procedure that would actually precisely identify the shape is changing the parametric description either into a function, or at least to some implicit equation that we recognize.

This is done by eliminating t from the description. Can we express t from one of the two equations above? The first equation looks quite inviting, so we can try it. We notice that we do not really need t itself, since we will want to substitute for t into the formula for y, but there this t is always as e^t, so it is enough to express this exponential from the first equation.

The equation y = x² − 1 defines an upward oriented parabola that crosses the x-axis at −1 and 1. The shape of the parametric curve is thus given by this parabola, but it need not be the whole parabola, depending on the parametrization. What can we say about values of x and y?

The expression x = e^t − 1 with t going through all real numbers has range (−1,∞), since always e^t > 0 and the exponential reaches all positive numbers. Thus for the parametric curve we only take the part of parabola given by x > −1.

How about the other coordinate? The expression y = e^2t − 2e^t is easier to analyze if we denote z = e^t and rewrite y as y = z² − 2z, that is, y = z(z − 2). What values can we obtain from this expression for z > 0? We can sketch the graph of this expression and see that it attains values between −1 (included) and infinity, which fits with the truncated parabola we arrived at in the previous paragraph.

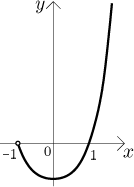
The conclusion is that the given parametric equations describe a piece of the parabola y = x² − 1 given by x > −1.

Back to Solved Problems - Implicit and parametric functions