Asymptotes: Survey of methods

We recognize three kinds of asymptotes: vertical, horizontal, and oblique. Note that formally, horizontal asymptotes actually belong among oblique ones, but for practical purposes it is better to treat them as a separate case.

Consider a function f.

Algorithm for vertical asymptotes:
Step 1. Identify points where the function might have vertical asymptotes. Suspicious points are: endpoints of intervals from the definition; endpoints of intervals of the domain; points where continuity is suspect.
Step 2. For each suspicious point a, find all one-sided limits at a that make sense (depends on which side of a the function is defined). If at least one of these limits is improper, then the function has a vertical asymptote at a (or put another way, the line x = a is a vertical asymptote of this function).
Note: If we try one one-sided limit and it is improper, we already have a vertical asymptote there and there is no need to calculate the second one-sided limit (if it makes sense at all).

Algorithm for horizontal asymptotes:
At infinity: If the function is defined on some neighborhood of infinity, find its limit at infinity. If this limit is proper and equal to L, then the line y = L is the horizontal asymptote of f at infinity.
At negative infinity: If the function is defined on some neighborhood of negative infinity, find its limit at negative infinity. If this limit is proper and equal to L, then the line y = L is the horizontal asymptote of f at negative infinity.

Algorithm for oblique (non-horizontal) asymptotes:
At infinity:
Step 1. If the function is defined on some neighborhood of infinity, find its limit at infinity. If this limit is proper or does not exist, we do not have an oblique asymptote at infinity. If it is improper, go to the next step.
Step 2. Find

If this limit diverges (or is zero), then f does not have an oblique asymptote at infinity. If it converges (and is not zero), go to the next step.
Step 3. Find

If this limit diverges, then f does not have an oblique asymptote at infinity. If it converges, then the line y = Ax + B is the (oblique) asymptote of f at infinity.

At negative infinity:
Step 1. If the function is defined on some neighborhood of negative infinity, find its limit at negative infinity. If this limit is proper or does not exist, we do not have an oblique asymptote at negative infinity. If it is improper, go to the next step.
Step 2. Find

If this limit diverges (or is zero), then f does not have an oblique asymptote at negative infinity. If it converges (and is not zero), go to the next step.
Step 3. Find

If this limit diverges, then f does not have an oblique asymptote at negative infinity. If it converges, then the line y = Ax + B is the (oblique) asymptote of f at negative infinity.

Example: Investigate asymptotes of

Solution: D( f ) = (−∞,−1) ∪ (−1,∞), the function is continuous.

Candidates for vertical asymptotes: the proper endpoint x = −1 is the only one. We check on one-sided limits:

We do not have to evaluate the second one-sided limit, we already know from this limit that f has a vertical asymptote at −1.

Asymptote at infinity: We check on the limit

This shows that there is no horizontal asymptote at infinity. However, there is a chance for an oblique one. We follow the algorithm.

There's still a chance.

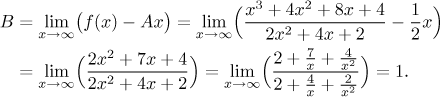
We conclude that the line y = x/2 + 1 is the asymptote at infinity.

Asymptote at negative infinity: We check on the limit

This shows that there is no horizontal asymptote at negative infinity. However, there is a chance for an oblique one. We follow the algorithm.

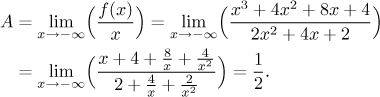
There's still a chance.

We conclude that the line y = x/2 + 1 is the asymptote at negative infinity.

By the way, if you want to see how this function looks like, check out the Example in Methods Survey - Graphing - Overview).

For more insight and another example see Asymptotes in Theory - Graphing, see also appropriate problems in Solved Problems.

Back to Methods Survey - Graphing functions