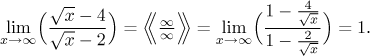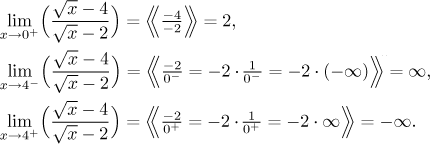Problem: Determine all asymptotes of
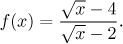
Solution: First we need to find the domain. There are two conditions,
the square root requires that
x ≥ 0
and the fraction does not allow the denominator to be zero, that is,
x = 4 is not allowed. Thus we have
D( f ) = [0,4) ∪ (4,∞).
Now we look for asymptotes. There is one place where a horizontal asymptote
might appear, at infinity. We find the limit there, for help with limits
see e.g. Limits in
Functions - Methods Survey.
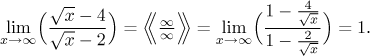
We have a proper limit, which shows that there is a horizontal asymptote
there, it has equation y = 1.
There is in general also a
chance for an oblique asymptote at infinity, but since we have the horizontal
one there, an oblique asymptote is not possible.
Vertical asymptotes might happen at proper endpoints of intervals of the
domain (in our case we have candidates x = 0 and
x = 4) and also at points of discontinuity, but
the given functions is continuous and no such points appear. Vertical
asymptotes are decided based on one-sided limits at candidate points.
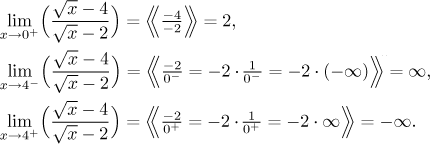
The one-sided limit at 0 from the right is proper, which means that there is
no vertical asymptote at x = 0.
We could have actually reached this conclusion without any calculation, the function is
defined and continuous at 0, therefore it necessarily must have a proper
limit there. On the other
hand, we have an improper limit at 4 (even both of them, but one would be
enough), so we know that there is a vertical asymptote at
x = 4.
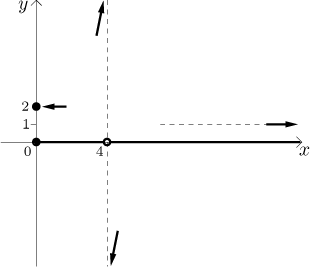
We can express the data that we found out in a sketch.
Next problem
Back to Solved Problems -
Graphing
![]()