Tangent and normal lines

There are many ways to determine the equation of a line in the plane. In our situation we will be looking for an equation of a line that passes through a certain point (a,b) and has the slope k. Then the equation reads

y − b = k⋅(x − a).

Since the point lies on the graph of the given function f, we have b = f (a). The slope of the line that is tangent to the graph is given by k_T = f ′(a) so that the line and the curve have the same direction at the touching point. Thus we get the equation of the tangent line:

y − f (a) = f ′(a)⋅(x − a).

How do we get the normal line? Its direction is perpendicular to the tangent direction, thus we get its slope using the following fact.

Fact.
Consider two lines in the plane whose slopes are k₁ and k₂. These two lines are mutually perpendicular if and only if k₁⋅k₂ = −1.

Thus we get the following formula for the slope of the normal line:

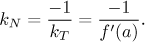
Consequently, the equation of the normal line is

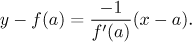
For an example see Tangent line in Methods Survey - Applications, check out also Solved Problems - Applications.

Note that the formula k_N = −1/k_T also includes the case when one of these slopes is infinity (a vertical line) and the other one is zero (horizontal line).

There are many ways in which one can write the equation of a line. Some people prefer the form y = A⋅x + B, others the form Ax + By = C. Since all forms are equivalent and it is easy to pass from one to another, there is no problem to get the form you like. The last form is popular also because it directly yields a normal vector to the given line, consequently also a directional vector. These vectors are useful when investigating geometry. How do we get such vectors?

If we know the slope k of some line, then its directional vector is B = (1,k). In particular, given a function f and a point a, then v = (1,f ′(a)) is the tangent vector to the graph of f at a. There are two useful special cases:

The tangent vector to an implicit curve F(x,y) = C can be also found as v = (dF/dy,−dF/dx).

The tangent vector to a parametric curve x = x(t), y = y(t) can be also found as v = (,).

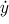Once we have a tangent vector (u,v), we obtain a normal vector easily as (v,−u).