Here we sum up the basic properties of integrals that are useful in calculations.
Newton integral or an indefinite integral of a given function f is the set of all antiderivatives F, we denote it
![]()
The Newton integral is linear:
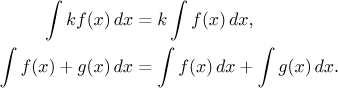
The Riemann (definite) integral corresponds to the mathematical area of the region under the graph of f, which is equal to the areas of the pieces above the x-axis minus the areas of the pieces below the x-axis. Elementary geometric reasoning then suggests that
![]()
The Riemann integral is also linear. In other words, it behaves reasonably when we multiply the integrated function by a number:
![]()
It also handles addition well:
![]()
It has useful comparison properties: Let f and g be Riemann
integrable functions on
![]()