First we define the notion of piecewise continuity:
Definition
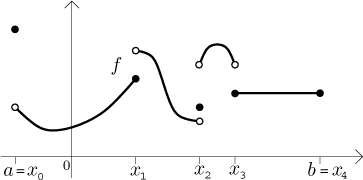
We say that a function f is piecewise continuous on an interval[a,b] if there is a finite set of pointsa = x0 < x1 < . . . < xN = b such that for every segment[xk−1,xk], wherek = 1,...,N, the function f has a limit atxk−1 from the right, limit atxk from the left, and is continuous on(xk−1,xk).
Here is a typical example of a piecewise continuous function:

We have the following statement:
Theorem
If a function is piecewise continuous on a closed interval, then it is Riemann integrable there.
Piecewise continuous functions are useful because they are often used in applications.
Actually, even infinitely many - but countably many - points of discontinuity do not pose a problem. The precise statement concerning how many points of discontinuity are allowed is this:
Theorem
A function defined on a closed interval is Riemann integrable there if and only if the set of its points of discontinuity is of measure zero.
The "measure" in this statement is the Lebesgue measure - which clearly shows that this is way beyond the scope of this Math Tutor.