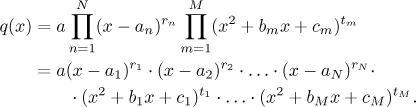Partial fractions
This method is used when working with rational functions, that is, ratios of
polynomials. Obviously, we will use it for integration here. Here it comes.
Theorem (partial fractions decomposition)
Let p and q be real polynomials, let the degree of
p be less than the degree of q. Assume that q can be
factored as follows:
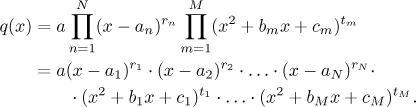
where the factors are mutually distinct and the quadratic terms are
irreducible (without real roots). Then we have the following decomposition:

and all the constants A, B a C are uniquely determined
by the denominator of the corresponding partial fraction.
What does it tell us? Imagine that we have two polynomials,
p(x) and q(x),
which determine a rational function
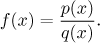
We may assume that this rational function is "proper", that is, the
polynomial in the numerator has a lower degree than the one in the
denominator. This theorem says that a problem that features perhaps even a
very complicated ratio can be reduced to ratios that are markedly simpler,
in fact they are chosen from two basic types, so-called partial
fractions.
For every linear factor
(x − a)n
of the denominator q(x) we get partial fractions
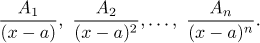
For every irreducible quadratic factor
(x2 + bx + a)n
of the denominator q(x) we get partial fractions
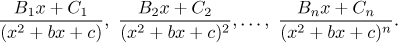
As an example convince yourself that the following equality is true.
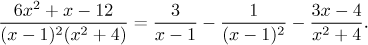
The theorem also says that the decomposition can be done in just one way. On
the other hand, it does not tell us how to find the coefficients in the
partial fractions, which is not so surprising, there are no universal
formulas for them. There are several methods for finding these numbers and
we will discuss it in the section on
rational functions in Methods
Survey - Methods of integration.
Back to Theory - Integration