Given: a proper rational function, that is, a ratio of polynomials
![]() such that
such that
![]()
Here all quadratic factors cannot be further factored into linear factors (they do not have real roots) and all factors in this decomposition are distinct.
The task is to decompose this ratio into a sum of partial fractions.
Algorithm for partial fractions decomposition.
Step 1. For every factor
![]()
For every factor
![]()
It is customary to denote constants not using indices but using successive letters. Here you find some examples that should clarify this proces of creating the decomposition. Note that the number of unknown letters is always the same as the degree of the denominator. Note also that the numerator p does not have any bearing on identity of partial fractions.
Step 2. Determine the unknown constants A, B, C,... appearing in partial fractions using the knowledge of p.
There are several methods for determining the unknown constants, we will now cover the most important ones. To illustrate them we consider the following function.
![]()
We start by decomposing the denominator as
![]()
Now we have to find constants A and B, we will show the most useful methods.
"Multiplying" method:
We multiply the equation given by the desired decomposition above by the
common denominator, cancel on the right hand-side (which is always possible)
and then multiply out. The last step is to gather all equal powers together
on the right so that there will be a polynomial with unknown coefficients.
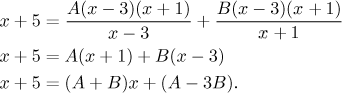
We have equality of two polynomials, which happens only if their coefficients are equal. Thus we obtain a system of linear equations
![]()
The solution is
![]()
This concludes the partial fractions decomposition. Incidentally, both partial fractions are easy to integrate (by using a linear substitution if necessary), so we get
![]()
This integral is valid on intervals not including numbers −1 and 3.
This trick is the only really reliable methods. It will always work, which makes it very important. The downside is that it can be very long and demanding for calculations by hand, because in general the number of unknowns and the number of equations we obtain is equal to the degree of the denominator.
Heaviside's "cover-up" method:
We start from the original equation:
![]()
If we want to determine A, we cover up the corresponding factor

Similarly, by covering up
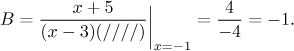
We are getting the same decomposition as before and essentially for free. This is the best method for finding unknown coefficients, an experienced decomposer would just write down the basic equality with general decomposition, then he would just cover up various parts with a finger and write the results right away. Try it for yourself:
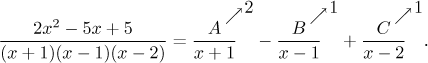
Since it will be obviously our favorite method, we look at it closer. Assume
that we have that ratio of polynomials
![]() and that
and that
![]()
The ratio
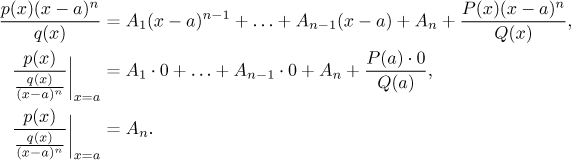
We obtained on the right the unknown coefficient
We can now also see the main limitations of this method. The first problem
occurs when n is larger than 1, since we are not able to obtain other
corresponding constants. For instance, in order to get
Example: Consider the following decomposition.
![]()
Note that x2 is not an irreducible quadratic factor but a
linear term
By covering up
Thus we turn to the reliable multiplying method, but since we already know two values, we need not solve a system of three equations, just one will suffice. This will simplify our work significantly.
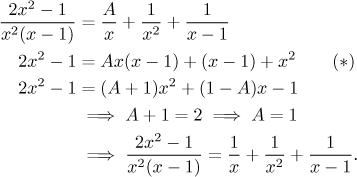
Similarly we proceed when there are quadratic factors present. This is the second limitation of the cover-up method, it cannot give us coefficients corresponding to quadratic factors. The reason is simple, there is no real root to substitute. We will show an example below, but first we sum it up.
Algorithm for determining coefficients of partial fractions.
Step 1. If there are any linear factors present, then for every
factor
a) Cover the factor
b) substitute
If the given function featuren only linear factors in power 1, you are done.
Step 2. If you obtained any coefficients in Step 1, substitute them
into the general decomposition you are looking for. Then find the remaining
coefficients using the multiplying method:
a) Multiply both sides of the decomposition by the common denominator,
cancel on the right,
b) rewrite the expression on the right as a polynomial,
c) comparing coefficients of polynomials on the left and on the right deduce
as many equations as there are unknowns to determine,
d) solve those equations. You are done.
Before we show another example, we will show two supplementary methods. They are not really necessary to know (the above algorithm usually works very well), but some people may appreciate that they make deducing equations in the multiplying trick easier.
"Plug in" method:
This method starts with the equation that we obtained by multiplying the
decomposition at the beginning of the multiplying method. In the above
example it is the equation denoted (*). This equality is supposed to be true
for all x, so in particular it must be true for a particular value
that we choose. So it we substitute some chosen number for x in this
equality, we get an equation with the unknown constants. We substitute as
many values for x as is the number of equations we need. There might
arise a complication if some equations happen to be dependent, but this we
find out while solving them and fix it easily by substituting yet another
value for x, thus getting another equation.
Substituting roots of linear facors is equivalent to the cover-up method. So if you used that method already before the multiplying method, then for the plug-in trick you need to choose other values than the roots.
Let us return tot he last example. If we substitute into (*) something
different from 0 and 1, say,
![]()
"Limit" method:
This method starts with the original decomposition equality. It consists of
rational functions and we know well how these behave at infinity. In our
equation all rational functions are proper, so the degrees in numerators
is smaller than degrees in denominators and therefore those ratios all go to
zero at infinity. However, there are always some fractions where the
numerator's degree is smaller exactly by one. If we multiply the basic
equation by x and then pass to infinity, we can easily determine
limits of all ratios. Those that have still smaller degree in the
numerator go to zero, whereas those that now have equal degrees tend to the
ratio of coefficients at highest powers. We again return to the above
example and try it, first multply all terms by x and then send
x to infinity.
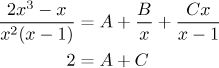
We obtained an equation almost for free, an experienced solver can do it without actualy writing the multiplied equality, just by looking at the original decomposition equality. Often this is enough, also here we already obtained other unknowns using the cover-up method, so we can deduce A right away and the decomposition is done.
As we wrote, these two supplementary methods are not really needed. Some students do not like it when things get complicated and they have to make decisions. These students are then happy with the algorithm above. They learn the over-up and multiplying methods and manage to solve all problems with it, even thought it sometimes takes longer calculations. We will respect this and do our basic solutions here in this way.
However, many students that feel really comfortable in this area are often confident enough to handle some more complicated decision making and they appreciate knowing a few tricks that can shorten calculations considerably. For those we introduced these two supplementary methods, we will use them where appropriate as optional solutions. There are many other tricks, a curious reader can find several more advanced but probably less practical methods in this note.
Example: Consider the following decomposition.
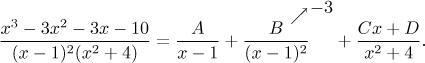
We were able to identify one coefficient using the cover-up method, we
covered up
![]()
Now the standard procedure is to multiply out the star-labeled equation, rewrite the right hand-side into a polynomial, then compare both sides and obtain four equations. The fact that we already know B will be helpful when we try to solve them:
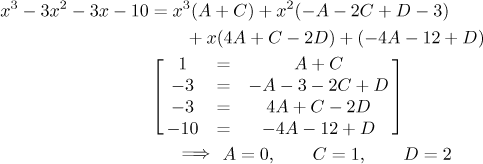
and therefore
![]()
How does the plug-in trick come in? Instead of multiplying out the right hand-side we can start with the equation (*) and obtain three equations (which is what we really need) by substituting in three values for x, preferably small.
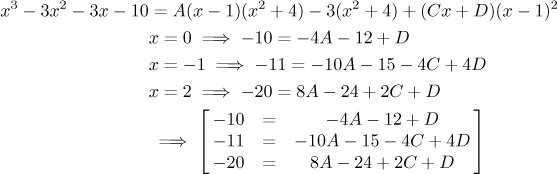
It seems that it was easier to get these three equations, on the other hand this procedure often yields equations with large coefficients, which is not so nice when it comes to solving them. As we already noted, this method is an option, take it or leave it.
Another optional method used limit. We multiply the basic equality by x and then pass to infinity.

It is just one equation, but it was almost for free. Note that it is the same equation as we obtained above in multiplying method when comparing coefficients at the highest power. This is no accident, it always works this way.
More partial fractions examples can be found in Solved Problems - Integrals; in fact, most problems there lead sooner or later to partial fractions, a typical decomposition is for instance in this problem.