Typical integrals:

Example	Box
	Substitution Here y = x5 − x.
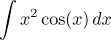	Integration by parts
	Integration by parts
	Substitution Here y = sin(x). It also fits the box "trigonometric integrals", but there the recommendation there is exactly the substitution as above.
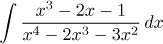	Rational function (partial fractions decomposition)
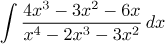	Rational function (partial fractions decomposition) Better: Substitution (numerator is the derivative of denominator).
	Integration by parts
	Substitution Here y = ln(x).
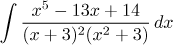	Rational function (partial fractions decomposition)
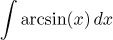	Integration by parts
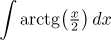	Integration by parts
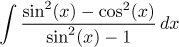	Trigonometric integral Either the universal substitution y = tan(x/2), or in this case also the easier y = tan(x).
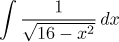	Integral with a root of a quadratic General method: indirect substitution x = 4sin(t). Here we have a simpler alternative: Factoring out the constant leads to an elementary integral.
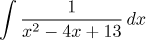	Rational function Completing the square and factoring out a constant leads to an elementary integral

A well-prepared student should make such associations on the fly. Note that although the list is by no means exhaustive, experience suggests that if a student is really familiar with integrals of the listed types, he should do well on most integration problems.