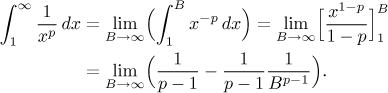Properties and examples of improper integrals
Since improper integrals are defined using a limit, most properties valid for
definite (Riemann) integrals are still true. In particular we have:
Fact.
(i) For all functions f,g and real numbers k we have
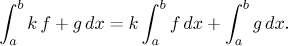
(ii) For all functions f and real numbers
a < b < c we
have

Each of these inequalities is understood in the following sense: If
integral(s) on one side are convergent, then so are the ones on the other
side and the two sides are equal.
(iii) Assume that f and g are functions whose integrals
from a to b
converge. If f ≤ g
on (a,b),
then
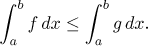
The third property is a basis for a test of convergence based on comparison.
This will be explained in the next section, however, we already see that it
should be possible to somehow rank functions according to how well their
integrals converge. This topic will be addressed now. We know that for
positive functions there are essentially two kinds of problems, integrals to
infinity and vertical asymptotes. We will start with the former.
Powers at infinity.
In the previous section
(Introduction to improper
integrals) we showed that
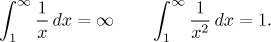
The scale of powers is perhaps the most important and we will look at them in
general. Since we know that to have any hope of a convergent integral at
infinity, the integrated function should tend to zero, it is natural to look
at powers in the following form:
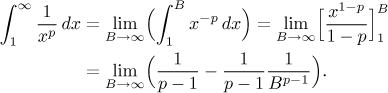
The limit converges if and only if p > 1.
Note that this calculation is not correct for the case
p = 1, when the integration yields logarithm,
but we already did this case
before,
getting a divergent integral. Thus we formally get
Fact (scale of powers, p-test).
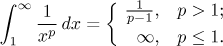
This picture should be helpful:
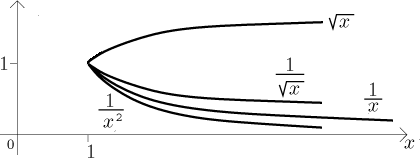
The area under the graph of 1/x is infinite. Naturally,
if we put a smaller power in the denominator, the graph will be higher, the
area larger and thus it still should be infinite. On the other hand, if we
put a higher power in the denominator, the graph will go down and the above
calculation shows that now the area is finite. In other words, the function
1/x is exactly the one where divergence changes into
convergence, the function itself giving a divergent integral.
This may be the right moment to note the difference in terminology and
meaning. Although the function 1/x itself is convergent
at infinity (namely, it tends to zero), its integral to infinity (for
instance from one as above) is divergent.
Note also another important thing. The convergence or divergence of the above
integrals cannot be influenced by the choice of the lower limit (as long as
it is greater than zero). This is quite natural, since these functions have
no problems other than 0 and infinity. If we remove a finite region from a
region of infinite area, the resulting region will still have infinite area.
Similarly, we cannot "spoil" a region of finite area by adding/subtracting a
finite region. This in fact follows from the property (ii) above. Of course,
if we, for instance, decide to integrate the above powers from 2 to infinity,
the convergent ones will have different answers (but cannot become infinity).
Powers at zero.
We again look at the easiest case, assuming that
p ≠ 1:

This time, the limit exists if and only if
p < 1. An easy calculation with logarithm
as antiderivative shows that also the integral with
p = 1 is divergent, hence we get

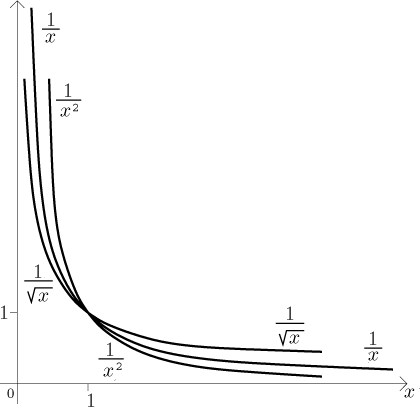
Thus we have the following picture:

Again, the function 1/x (with divergent area under it)
is the border case between convergence and divergence. Note that the powers
in fact work as "levers". We can start with the graph of
1/x, which has infinite areas at "both ends", at
0 and infinity. If we increase the power, the right end goes down
(convergent integral) and the left one up (divergent integral). If we
decrease the power, the situation is reversed.
There are functions that look similar and have convergent integrals both at 0
and at infinity; in other words, if we integrate them from 0 to infinity
(which then must be done by splitting it into two integrals), it comes out
convergent. The above considerations show that simple powers would not do
this, one has to try something more complicated.
Problems at other places can be explored similarly. The situation at negative
infinity is about the same as at infinity (with the difference that not all
powers are defined on the negative half-axis). Also the behaviour at zero
from the left is the same as the behaviour at zero from the right, with the
same problem of some powers not being defined there. Vertical asymptotes at
other points are mere shifts of the vertical asymptote situation at zero.
Thus, for instance,

but now this is only true for p's for which the power is defined on
(1,2), for instance for p = 1/3
it works, but for p = 1/2 it does
not make sense.
Convergence tests
Back to Theory - Improper Integrals
![]()
![]()
![]()