Average of a function

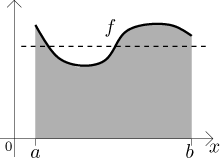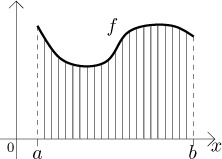
Let f be a function on an interval [a,b]. We want to calculate its average. We know how to find the average of a finite number of elements - we add them up and divide by their number. We try to apply this idea to a function on an interval.

Divide the interval [a,b] into disjoint subintervals of size dx (see here for explanation of dx) and divide the region under f into corresponding vertical strips.

Since these subintervals are so thin, the change of f within each of them can be ignored. Therefore the average of f can be obtained by finding the average of heights of all these strips. How many such strips do we have? This is easy, each strip is dx wide and the total must give the size of the interval [a,b]. Thus the average of f should be

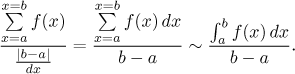
This leads us to the following definition of the average of a given function, also called its mean (value):

Definition.
Let f be a Riemann integrable function on [a,b]. We define the average of f over this interval by

Note that we get

This is interesting for two reasons. First, by the Mean value Theorem for integrals, if f is continuous, then it must attain its average at some point of [a,b]. Note that the continuity is crucial. Indeed, recall the example of a jump function we saw before. Its average over [0,2] is 3/2, but the function is never equal to 3/2.

The above equality is also interesting from the geometric point of view. Is says the following: If we look at the region under the graph of f and flatten its top at the level of the average of f, the resulting rectangle has the same area as the region under the graph of f.

Area
Back to Theory - Applications