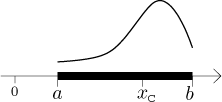
Consider a segment

Its mass is given by
![]()
The centre of mass lies on the x-axis and its x-coordinate is
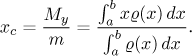
(Here
Consider the graph of a function F on an interval
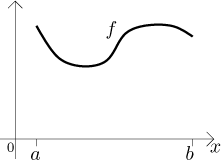
The mass of this curve is given by
![]()
Its centre of gravity has coordinates
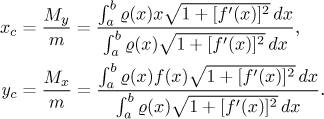
(Here M are the moments of rotation with respect to the respective axes.)
Consider a plane region bounded from above by the graph of a function
f and from below by the graph of a function g on an interval
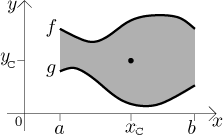
The mass of this region is given by
![]()
The centre of mass is given by
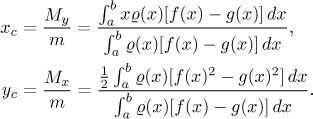
(Here M are the moments of rotation with respect to the respective axes.)
Consider the plane region bounded from above by the graph of a function
f and from below by the graph of a positive function g on an
interval
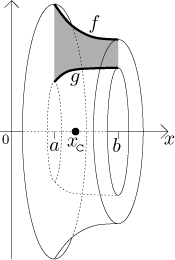
If the region is rotated about the x-axis, the resulting solid has the mass
![]()
The centre of mass lies on the x-axis and its x-coordinate is
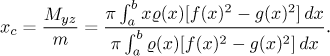
(Here
Note that in all these situations, the most usual setting is when the
material is homogeneous, that is, the density is always the same. In such a
case the density function
Consider a parametric curve
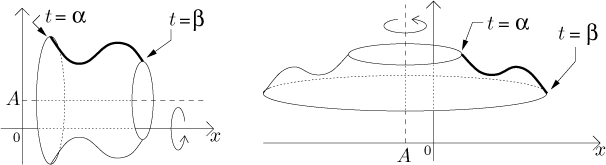
For simplicity we will only consider homogeneous objects. Theor mass can then be calculated as their length/area/volume (see corresponding sections) multiplied by the given constant density. Now we will look at density, in the formulas the density will cancel out.
The center of gravity of the curve itself has coordinates

The center of gravity of the region under this curve has coordinates

The center of gravity of the surface obtained by revolving this curve about the x-axis lies on this axis and its x-coordinate is
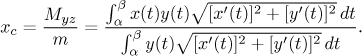
The center of gravity of the solid obtained by revolving the region under this curve about the x-axis lies on this axis and its x-coordinate is
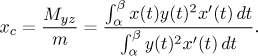
Note that in the last two fractions we cancelled
Derivative of an integral
Back to Methods Survey
- Applications