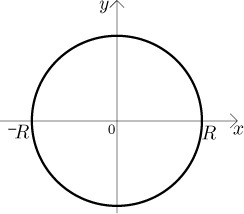
Problem: Find the area of a disc of radius R.

Solution: We position the disc with its center in the origin:

First we will try it using the graph of a function approach. Since the picture is symmetric, the area of the disc is equal to the double of the area of the upper half. What function has its graph equal to an upper semi-circle? Since the circle is given by x² + y² = R², we get (for the upper half)

Thus the area of the circle is

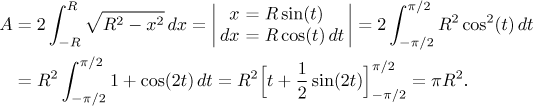
Note that the integral was a standard type from the "root of quadratics" box.

The centered circle of radius R can be also described by parametric equations x = Rcos(t), y = Rsin(t), for t between -π and π (for instance). But to find the area, we have to take a part where x is monotone, so we will again take the area of the upper half, which corresponds to t ranging from 0 to π, and then double it.

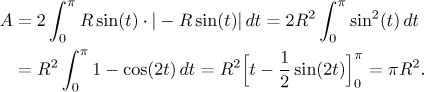
Finally, we can try do pass to polar coordinates. The centered circle of radius R is given by the equation ϱ(φ) = R for φ ranging for instance between 0 and 2π. The area between this curve and the origin is then

Since circle is an object invariant with respect to rotation about the origin, it is not surprising that the polar coordinates lead to the easiest solution.

Next problem
Back to Solved Problems - Applications