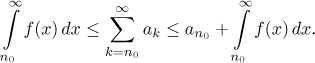
We cover two topics here.
1. Theoretical estimation of the sum of a given series.
Here the main tool is the
Integral test, see Theory -
Testing convergence. If the terms ak of a given
series come from some positive and non-increasing function f as
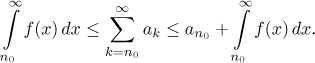
For an example see Integral test in Theory - Testing convergence.
2. Estimation of error when approximating series by finite sums.
This can be often done by applying the above estimate to the tail of the given series. In combination with comparison (see Comparison tests in Theory - Testing convergence) we get a more general statement.
Consider a convergent series
of real numbers. ak
• If there is a series∑ bk and an integer N such that|ak| ≤ bk fork > N, then
• If there is a positive non-increasing function g and an integer N such that
|ak| ≤ g(k) fork > N, then
Example: We want to approximate the sum of the series
by its partial sum with precision 0.0001.
What is the error of approximation of the sum of this series by the first N terms? Using the first approach we can get rid of the annoying "+1" part.
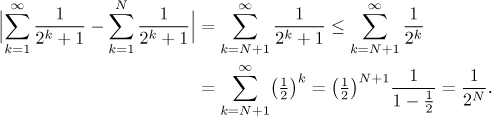
Now we just find what N will make the resulting error estimate at most 0.00001, so the answer is that N = 17 is enough. Thus we sum up the first 17 terms of the given series and we already know its sum with the given precision.
For an example on using the second approach via a function see the example in Integral test in Theory - Introduction and this problem in Solved Problems - Summing up series.
In general, we can attempt to estimate the error series (in absolute value) from above by any other convergent series whose sum we are able to determine, often this involves a geometric series. See this problem in Solved Problems - Summing up series.
We also have an estimate for alternating series.
Consider a series
of real numbers. Assume that ak = (−1)kbk for some non-increasing sequence{bk} of positive numbers that tends to zero. Then
For an example see this problem in Solved Problems - Summing up series.
