Integral test: Methods survey

The Integral test is used as follows.

Algorithm:
We are given a series  ∑ a_k  with positive terms. Assume that the terms a_k are given by an expression that also defines some positive and non-increasing function f (x) on some interval [K,∞).
Evaluate improper integral  . The conclusion (whether it converges or not) also applies to the series  ∑ a_k.

One also gets an estimate, see Integral test in Theory - Testing convergence.

When is this test useful? If we look at the given series and like the idea of integrating instead of summing, then this test is the obvious choice - of course assuming that the function in question is non-increasing.

Example: Decide on convergence of the series

Since the function f (x) = 1/(x² + 1) is positive and decreasing for x ≥ 0, the formal assumptions of the Integral test are satisfied and we can check on the corresponding improper integral.

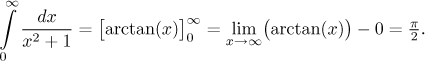
Since this integral converges, by the Integral test also the given series converges.

For other examples see this problem and this problem in Solved Problems - Testing convergence.

Back to Methods Survey - Testing convergence