Příklad: Vyšetřete konvergenci následující posloupnosti funkcí:

Řešení: Nejprve se podíváme na bodovou konvergenci. Budeme považovat x za parametr a spočítáme limitu vzhledem ke k. Protože ten sinus v čitateli je v absolutní hodnotě omezený číslem 1 a jmenovatel jde do nekonečna, dostáváme

Formálně se dá použít například srovnání.

Závěr: Daná posloupnost konverguje k funkci f (x) = 0 na celé reálné ose (což je tedy obor konvergence této posloupnosti).

Jak je to se stejnoměrnou konvergencí? Začneme zkoumáním rozdílu mezi f a jednou konkrétní f_k na právě zjištěném oboru konvergence.

Právě jsme dokázali stejnoměrnou konvergenci.

Závěr: Daná posloupnost konverguje k funkci 0 stejnoměrně na celé reálné ose.

Požádal jsem počítač o několik obrázků, abychom alespoň přibližně naznačili, co se tu děje.

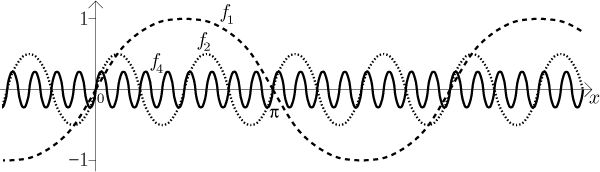
Tento příklad je tak snadný, že se asi divíte, pro to tu ukazujeme; určitě na tomto příkladu musí být něco víc. A taky že ano, což rychle zjistíme, když zkusíme derivovat.

S výjimkou bodu x = 0 tato posloupnost derivací dokonce ani nekonverguje pro k jdoucí do nekonečna, tím spíš nejde k 0 neboli k f ′.

Abychom to shrnuli, máme funkce f_k, které konvergují stejnoměrně k f na libovolném intervalu v kladné poloose, ale f_k′ nekonvergují k f ′ na žádném takovém intervalu, dokonce ani ne bodově. To ukazuje, že derivování řad je opravdu choulostivá záležitost.

Další příklad
Zpět na Řešené příklady - Řady funkcí